As the whole set of posts covering this whole topic is difficult to follow in sequence due to the nature of the blog format, and as it all involves many calculations, a brief summary post may help!
1. The Reshel system as defined by William S. Buehler, which came to my awareness in the late nineties. This was based on a 20 mile radius centred on St. Mary's Chapel Mount Lothian in Scotland, NT 275 570.
This radius I have since amended to 19.596 miles, being the side of a square with diagonal the same as that of the grid identified on the island of Bornholm which Haagensen and Lincoln show (and prove) to be a Secret Teaching Island of the Knights Templar. This grid in Imperial measure is (16 times the square root of 3) which equals 27.712813 miles (E).
This measure was found to be the exact distance between St. Mary's Chapel and St. Baldred's Chapel on The Bass Rock, NT 602 873.
This as diagonal of a square is in (square root two) relationship with the side, hence the 19.596 miles(E) radius mentioned above, which is the distance approximately to Seafield Tower, NT 279 885, to the north and Dryhope Tower, NT 267 247, to the south. (The double distance between the two Towers giving the diameter of the circle, which is 39.192 miles(E).)
Using the simple geometry of circles and squares, an inner square grid can be constructed naturally, with side half that of the original, 13.8564 miles (E).
2. Using this smaller grid with St. Mary's Chapel as centre, Blackness Castle defines the diagonal approximately, as example, NT 055 802.
It was then found from this grid that a point near Kelso, NT 716 340, and a point near Ericstane, NT 051 116, are both (2 by 1) diagonal points from St. Mary's Chapel, and are naturally a (3 by 1) diagonal distance apart from each other.
Using this as a baseline a line at 90 degrees from the mid-point through St. Mary's Chapel and extended north west is also naturally on a (3 by 1) diagonal, and it is on this line that a system is found corresponding nicely to the basic Reshel format as described by William Buehler.
N.b.: it needs to pointed out here that the orientation of the Bass Rock is some 2.4 degrees clockwise to that of the Rose-line/Tavhara line as commonly understood, and that there is a third in between using Berwick Law NT 556 842, which is used for the following excercise.
This spread of 2.4 degrees could be considered as a 'Selah' spoke, and as the geometry which gives the points below is accurate to the metre, an area of fudge could be considered at all points corresponding to this 2,4 degree spread but centred at St. Mary's Chapel.
3. A) The first point of note on this axis is St. Mary's Chapel itself, as it is naturally the point defining a square with the base-line as diagonal. From Pythagoras' theorem, a triangle with two sides equal to (square root five),which the diagonal of a (2 by 1) rectangle naturally is, with the third side (square root ten), that is the diagonal of a (3 by 1) rectangle, is a right angled triangle, with angles of 45 degrees. The other half of the square is to the south of the base-line, of course! This will be discussed later!
B) The second point on the axis, (and the clincher for me!) is Hillend Fort NT 245 662 which is at the point corresponding to the apex of the Great Pyramid, or Glory Pole in WSB's terminology for the system, 51.86416667 degrees, or 51 degrees, 51 minutes, 51 seconds. I have made many references to the significance of Hillend Fort in the landscape of Lothian, prior even to discovering this fact.
C) The point which defines an equilateral triangle with the base-line is in the Firth of Forth, with Inchmickery and Inchcolm NT 191 826, the nearest islands.
D) There is a pentagon super-imposed with side defined by the tangent from St. Mary's Chapel intersecting the circle with Hillend Fort as radius from the centre of the base-line, and dropping a perpendicular to the base-line, either side of the mid-point of the base-line. The two base line points are NT 116 150, Craigy Middens at Ask Law, and NT 646 318, near Rutherford Lodge, a 67 metre spotheight by a boathouse on the River Tweed at Dalcove.
The apex of this pentagon is to the north of Loch Leven in the village of Milnathort, on Pace Hill NO 123 051. Burleigh Castle is close by at NO 129 047, some half kilometer east.
The 'wings' of the pentagon have points at; i)in the west at NS 793 603, the junction of Biggar and Motherwell Roads, and; ii)in the east at sea NT 651 874, off St. Baldred's Boat in the vicinity of the Bass Rock and Tantallon Castle. St. Baldred's Chapel on the Bass Rock is of course one of the points where this grid originated.
The mid-point of this penta-chord is at Craigleith Avenue, NT 222 738, in Edinburgh near Mary Erskine's school at Ravelston.
The centre of the pentagon is found to be just south of Rosslynlee Hospital at NT 266 599, near a claypit.
Tuesday 16 December 2008
Friday 28 November 2008
Friday 7 November 2008
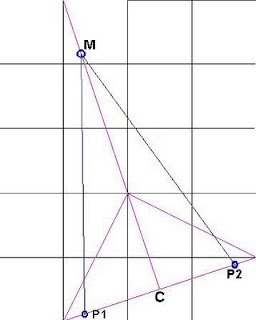
St. Mary's Chapel grid 3 by 1 diagonal pentagon
In the Reshel basic system shown by William Buehler is a pentagon constructed within the base-line, and this drawing shows my geometric interpretation, based on Bill's drawings.A tangent drawn horizontally from St. Mary's Chapel intersects a circle of radius C - H, centre of base-line to Hillend Fort or G.P apex point. Then a perpendicular is dropped to the base-line defining point P1.

Using the theorem of Pythagoras C-P1 = sq.root[{CG^2) - (CS^2)], where CG is the same as the radius CH, and CS equals the half-base EC;
Using figures calculated in previous post this gives a distance of 17,283343miles(E), or 278.15 O.S. units.
This line extended the same distance towards Kelso through C, gives point P2.
These two points can be determined by calculating the x and y coordinates as before, and subtracting from C for P1 and adding to C for P2:
x: cos17.4742 * 278.15 = 265.32
y: sin17.4742 * 278.15 = 83.52
P1:
x: C-265.32 = 3380.88 - 265.32 = 3115.56
y: C- 83.52 = 6233.87 - 83.52 = 6150.35
P2:
x: C+265.32 = 3380.88 + 265.32 = 3646.20
y: C+ 83.52 = 6233.87 + 83.52 = 6317.39
P1 proves to be Craigy Middens on Ask Law (NT 115 150).
P2 proves to be near a 67 metre spot height at Rutherford Lodge on a bend in the river Tweed at Dalcove (NT 646 317).
Now that the base points are established, the altitude of the pentagon can be calculated.
This is most easily done by using the tangent of 72 degrees multiplied by the half base measure, and oriented to the 17.4742 degree angle. Reminder; The 3 by 1 angle adjusted for the North Berwick Law orientation!
So, MC = tan72 * 278.15 = 856.07 O.S. units
x: C - sin17.4742 * 856.07 = 3380.88 - 257.06 = 3123.82
y: C + cos17.4742 * 856.07 = 6233.87 + 816.56 = 7050.43
This point is Pace Hill(NO124 050), in Milnathort, on the north shore of Loch Leven. Of interest perhaps is Burleigh Castle(NO129 047) some 0.5 KM east.
The line from C to M crosses Loch Leven between Kinross House and Loch Leven Castle Island. Loch Leven also contains St Serf's Island. The line also crosses Benarty Hill to the south, near to the fort there. This latter high point is visible from Hillend Fort, south of the Firth of Forth, and of course the G.P. angle point and much more!
Next, the 'wings' of the pentagon can be calculated using the same methods as before, but the workings are omitted here. The two points are given here labelled W(west) and E(east):

W: 2792.71 6603.40, which is at a crossroad of the Biggar Road, Motherwell Road near Pickerston, (NS793 603).
E: 3651.31 6873.68, in the North Sea, near to St.Baldred's Boat(NT611 849), marked rocks near Seacliff, with St. Baldred's Cave at (NT604 845), with Tantallon Castle close by. St. Baldred's Chapel on The Bass Rock is of course the origin of the grid with St. Mary's Chapel.
The chord of the pentagon between W and E cuts the altitude line at Ravelston in Edinburgh near to Mary Erskine's School(NY218 740) at 3222.01 6738.54.
One other point of the pentagon to be considered is the centre O which is at 3265.92 6599.05, near clay pits just south of Rosslynlee Hospital(NT265 608).
Coincidentally, or otherwise, the distance from O to St. Mary's Chapel calculates to 1.88 miles(E). The distance of 188 miles(E) and (S) was found to be the measure of the sides of the triangle described in previous post from Preston Cross to Flodagh and Callanish respectively.
There are other points or poles that can be determined but for now the main geometrics have been established for one half of the basic Reshel system as defined by William Buehler, and other points on the altitude which may be of interest. And, this is only one half of the system, a mirror system on the other side of the base line should be considered, and that can be done later. For me this system based on the grid found on Bornholm and then in Scotland using the 3 by 1 diagonals and the simple way of determining especially the Great Pyramid point, Hillend Fort, is the clincher. As previously mentioned Hillend Fort is a most important geometric point in the landscape. Inchcolm island being close to the equilateral triangle point is also good. And, that the altitude passes through the gap between Kinross House and Loch Leven castle island, with Benarty Hill giving a good line of sight point is also very impressive. Bearing in mind that the orientation used is that to Berwick Law, with a spread of a degree or so either side, the gap between Kinross House and Loch Leven Castle could be considered as a 'gate' through which the three options pass is interesting. Kinross House is designed looking out to the Castle island with the path leading from the House to the shore points directly towards the island.
The Kelso area is also interesting, with the Abbey, Roxburgh Castle and Floors Castle forming a triangle containing the three options. The Ericstane/Devils Beef Tub area at the other end of the base line is also intriguing, not least because the Rivers Tweed and Annan have their sources there. Kelso also has the Tweed passing through it and where the Teviot joins the Tweed. The Tweed also runs along the Phi-latitude roughly, the title of this blog.
With this exercise I have reached a stage which has taken me so long, due to my personal need to prove to myself that the method I employ is mathematically OK, and just getting the photos and graphics together has also taken time.
I have a few things I need to do yet, and as mentioned above there is still more to do on this system, but for now I can draw relax a bit, go over what I have already done here and improve things a bit. There are also some things to consider as a result of this exercise which I also need to look at. There is one issue I left unfinished way back, that I can now return to also. Another grid, quite specific in the Esk Valley, which contains a feature I have known about for some nine years now, but have not shown here yet, as I needed to establish the full set of geometric systems I have found over the 15 years now I have been researching this subject before speculating further on the who, when and why questions, although a few people have been aware of some of this work. Some have grown impatient with my lack of progress, I guess, but I needed to do this stuff in a way that I felt was necessary.
For me this goes beyond 'mere' ley-lines as commonly perceived. The geometry, IMHO is too accurate, too specific, beyond that considered by some other researchers to be necessary. The work of Henry Lincoln at Rennes Le Chateau is questioned by some, but the work he and Erling Haagensen did on Bornholm shows that there would appear to have been some kind of 'school' system unbeknown to most, working to the same accuracy as I have adopted in Scotland. Then there is the work of William Buehler and the explanations he gives, which I have been aware of for nine years now also, which is still beyond my understanding. Also, as complex and accurate as these systems are, the use of line of sight points, high points in the landscape show how simply it could all be surveyed. Simple, perhaps, but the overall design so complex, covering all of Scotland and incorporating Scottish and English/Imperial measure, and even the metric to some extent, allowing for the slight inaccuracy of the metre as originally calculated. The fact that the foot is such an accurate measure relating to the equatorial circumference of the earth is still an issue to be resolved: (360 * 365.242 * 1000)/ 5280 = 24,902.864 miles(E) which is accurate to within a mile of most authoritative estimates. Who calculated this, when and how???

Using the theorem of Pythagoras C-P1 = sq.root[{CG^2) - (CS^2)], where CG is the same as the radius CH, and CS equals the half-base EC;
Using figures calculated in previous post this gives a distance of 17,283343miles(E), or 278.15 O.S. units.
This line extended the same distance towards Kelso through C, gives point P2.
These two points can be determined by calculating the x and y coordinates as before, and subtracting from C for P1 and adding to C for P2:
x: cos17.4742 * 278.15 = 265.32
y: sin17.4742 * 278.15 = 83.52
P1:
x: C-265.32 = 3380.88 - 265.32 = 3115.56
y: C- 83.52 = 6233.87 - 83.52 = 6150.35
P2:
x: C+265.32 = 3380.88 + 265.32 = 3646.20
y: C+ 83.52 = 6233.87 + 83.52 = 6317.39
P1 proves to be Craigy Middens on Ask Law (NT 115 150).
P2 proves to be near a 67 metre spot height at Rutherford Lodge on a bend in the river Tweed at Dalcove (NT 646 317).
Now that the base points are established, the altitude of the pentagon can be calculated.
This is most easily done by using the tangent of 72 degrees multiplied by the half base measure, and oriented to the 17.4742 degree angle. Reminder; The 3 by 1 angle adjusted for the North Berwick Law orientation!

So, MC = tan72 * 278.15 = 856.07 O.S. units
x: C - sin17.4742 * 856.07 = 3380.88 - 257.06 = 3123.82
y: C + cos17.4742 * 856.07 = 6233.87 + 816.56 = 7050.43
This point is Pace Hill(NO124 050), in Milnathort, on the north shore of Loch Leven. Of interest perhaps is Burleigh Castle(NO129 047) some 0.5 KM east.
The line from C to M crosses Loch Leven between Kinross House and Loch Leven Castle Island. Loch Leven also contains St Serf's Island. The line also crosses Benarty Hill to the south, near to the fort there. This latter high point is visible from Hillend Fort, south of the Firth of Forth, and of course the G.P. angle point and much more!
Next, the 'wings' of the pentagon can be calculated using the same methods as before, but the workings are omitted here. The two points are given here labelled W(west) and E(east):

W: 2792.71 6603.40, which is at a crossroad of the Biggar Road, Motherwell Road near Pickerston, (NS793 603).
E: 3651.31 6873.68, in the North Sea, near to St.Baldred's Boat(NT611 849), marked rocks near Seacliff, with St. Baldred's Cave at (NT604 845), with Tantallon Castle close by. St. Baldred's Chapel on The Bass Rock is of course the origin of the grid with St. Mary's Chapel.
The chord of the pentagon between W and E cuts the altitude line at Ravelston in Edinburgh near to Mary Erskine's School(NY218 740) at 3222.01 6738.54.
One other point of the pentagon to be considered is the centre O which is at 3265.92 6599.05, near clay pits just south of Rosslynlee Hospital(NT265 608).
Coincidentally, or otherwise, the distance from O to St. Mary's Chapel calculates to 1.88 miles(E). The distance of 188 miles(E) and (S) was found to be the measure of the sides of the triangle described in previous post from Preston Cross to Flodagh and Callanish respectively.
There are other points or poles that can be determined but for now the main geometrics have been established for one half of the basic Reshel system as defined by William Buehler, and other points on the altitude which may be of interest. And, this is only one half of the system, a mirror system on the other side of the base line should be considered, and that can be done later. For me this system based on the grid found on Bornholm and then in Scotland using the 3 by 1 diagonals and the simple way of determining especially the Great Pyramid point, Hillend Fort, is the clincher. As previously mentioned Hillend Fort is a most important geometric point in the landscape. Inchcolm island being close to the equilateral triangle point is also good. And, that the altitude passes through the gap between Kinross House and Loch Leven castle island, with Benarty Hill giving a good line of sight point is also very impressive. Bearing in mind that the orientation used is that to Berwick Law, with a spread of a degree or so either side, the gap between Kinross House and Loch Leven Castle could be considered as a 'gate' through which the three options pass is interesting. Kinross House is designed looking out to the Castle island with the path leading from the House to the shore points directly towards the island.
The Kelso area is also interesting, with the Abbey, Roxburgh Castle and Floors Castle forming a triangle containing the three options. The Ericstane/Devils Beef Tub area at the other end of the base line is also intriguing, not least because the Rivers Tweed and Annan have their sources there. Kelso also has the Tweed passing through it and where the Teviot joins the Tweed. The Tweed also runs along the Phi-latitude roughly, the title of this blog.
With this exercise I have reached a stage which has taken me so long, due to my personal need to prove to myself that the method I employ is mathematically OK, and just getting the photos and graphics together has also taken time.
I have a few things I need to do yet, and as mentioned above there is still more to do on this system, but for now I can draw relax a bit, go over what I have already done here and improve things a bit. There are also some things to consider as a result of this exercise which I also need to look at. There is one issue I left unfinished way back, that I can now return to also. Another grid, quite specific in the Esk Valley, which contains a feature I have known about for some nine years now, but have not shown here yet, as I needed to establish the full set of geometric systems I have found over the 15 years now I have been researching this subject before speculating further on the who, when and why questions, although a few people have been aware of some of this work. Some have grown impatient with my lack of progress, I guess, but I needed to do this stuff in a way that I felt was necessary.
For me this goes beyond 'mere' ley-lines as commonly perceived. The geometry, IMHO is too accurate, too specific, beyond that considered by some other researchers to be necessary. The work of Henry Lincoln at Rennes Le Chateau is questioned by some, but the work he and Erling Haagensen did on Bornholm shows that there would appear to have been some kind of 'school' system unbeknown to most, working to the same accuracy as I have adopted in Scotland. Then there is the work of William Buehler and the explanations he gives, which I have been aware of for nine years now also, which is still beyond my understanding. Also, as complex and accurate as these systems are, the use of line of sight points, high points in the landscape show how simply it could all be surveyed. Simple, perhaps, but the overall design so complex, covering all of Scotland and incorporating Scottish and English/Imperial measure, and even the metric to some extent, allowing for the slight inaccuracy of the metre as originally calculated. The fact that the foot is such an accurate measure relating to the equatorial circumference of the earth is still an issue to be resolved: (360 * 365.242 * 1000)/ 5280 = 24,902.864 miles(E) which is accurate to within a mile of most authoritative estimates. Who calculated this, when and how???
Friday 31 October 2008
St. Mary's Chapel grid - 3 by 1 diagonal
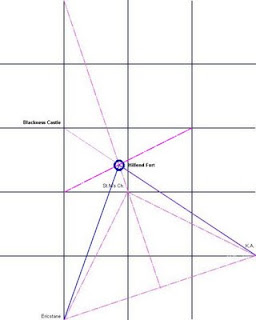
In this post I shall describe the first two elements of the 'Reshel' basic grid, which is the work of William S. Buehler, previously mentioned, constructed by me on the 3 by 1 diagonal system shown in the previous post.
The first element is the Great Pyramid triangle from the two base points, Kelso and Ericstane:

This point proves to be Hillend Fort(HF), a very significant point in the landscape mentioned previously.
The simplest way to calculate this point is to use trig. function tangent of the Great Pyramid angle, 51d 51m 51s, or 51.86416667 degrees, multiplied by the distance Ericstane(E) to base centre(C), to obtain the point on the axis through St. Mary's Chapel(SM):
For this exercise I have used the St. Mary's Chapel(SM) - North Berwick Law(NBL) orientation which gives a 3 by 1 diagonal to O.S grid of 17.4742 degrees, for now, as it is between the other two options, the Bass Rock, and the Roseline through Arthur's Seat.
The distance from E - C is [{16*sq.rt.3}/2]*(sq.rt.10)/2, which is 21.909miles(E), or 352.59 O.S units, (hundred metres)
tan 51.86416667 * 352.59 = 449.10 O.S.units.
The x and y components can be calculated using the 17.4742 deg. offset angle.
x: sin 17.4742 * 449.10 = 134.85 O.S.grid units
y: cos 17.4742 * 449.10 = 428.38 O.S.grid units.
The calculated base mid - point(C) at this orientation was calculated as 3380.88 6233.87; approximately NT 381 234.
Due to the north west north slant the x component will be subtracted, the y component added:
x: 3380.88 - 134.85 = 3246.03
y: 6233.87 + 428.38 = 6662.25
I have Hillend Fort(NT 245 662) as 3245.50 6662.25 universal O.S. grid coordinates, a mere 50 metres west on the x-axis, and exact on the y-axis. The Roseline orientation would take this towards the west a tad. I will get back to this later, to check!
This second graphic shows two grid connections for this point to within fractions of a degree, which could be used for any practical purpose, for this awkward point.
The line from KA(Kelso approx.)through Hillend coincides with the 2 by 3 diagonal to Blackness Castle, and as can be seen the 2 by 1 diagonal connects at the same point.
I have just noticed the 2 by 1 connection, which only reinforces my opinion of the importance of Hillend Fort, and even more convinced of the practicality of using the 3 by 1 grid diagonal, and indeed this particular grid. Found on Bornholm, applied to Scotland, and defining a specific, and very special point in the construct provided by William Buehler. Wow!
This third drawing is simple in comparison. It is the point which forms an equilateral triangle with the two base points.
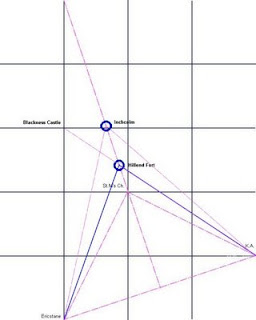
Again using the half base length, 352.59 O.S units and the tangent of 60 degrees, defines the point on the axis:
Tan 60 * 352.59 = 610.70 O.S. units
x and y components found using the offset angle of 17.4742 degrees:
x: sin 17.4742 * 610.70 = 183.38 O.S. units
y: cos 17.4742 * 610.70 = 582.52 O.S. units
and again using base centre:
x: 3380.88 - 183.38 = 3197.50
y: 6233.87 + 582.52 = 6816.39
Oxcars (NT 202 817) a tiny island in the Forth is the nearest land, about 0.5 km, but the line clips Inchcolm at the eastern end, a distance of approx 0.75 km.
The first element is the Great Pyramid triangle from the two base points, Kelso and Ericstane:

This point proves to be Hillend Fort(HF), a very significant point in the landscape mentioned previously.
The simplest way to calculate this point is to use trig. function tangent of the Great Pyramid angle, 51d 51m 51s, or 51.86416667 degrees, multiplied by the distance Ericstane(E) to base centre(C), to obtain the point on the axis through St. Mary's Chapel(SM):
For this exercise I have used the St. Mary's Chapel(SM) - North Berwick Law(NBL) orientation which gives a 3 by 1 diagonal to O.S grid of 17.4742 degrees, for now, as it is between the other two options, the Bass Rock, and the Roseline through Arthur's Seat.
The distance from E - C is [{16*sq.rt.3}/2]*(sq.rt.10)/2, which is 21.909miles(E), or 352.59 O.S units, (hundred metres)
tan 51.86416667 * 352.59 = 449.10 O.S.units.
The x and y components can be calculated using the 17.4742 deg. offset angle.
x: sin 17.4742 * 449.10 = 134.85 O.S.grid units
y: cos 17.4742 * 449.10 = 428.38 O.S.grid units.
The calculated base mid - point(C) at this orientation was calculated as 3380.88 6233.87; approximately NT 381 234.
Due to the north west north slant the x component will be subtracted, the y component added:
x: 3380.88 - 134.85 = 3246.03
y: 6233.87 + 428.38 = 6662.25
I have Hillend Fort(NT 245 662) as 3245.50 6662.25 universal O.S. grid coordinates, a mere 50 metres west on the x-axis, and exact on the y-axis. The Roseline orientation would take this towards the west a tad. I will get back to this later, to check!
This second graphic shows two grid connections for this point to within fractions of a degree, which could be used for any practical purpose, for this awkward point.
The line from KA(Kelso approx.)through Hillend coincides with the 2 by 3 diagonal to Blackness Castle, and as can be seen the 2 by 1 diagonal connects at the same point.

I have just noticed the 2 by 1 connection, which only reinforces my opinion of the importance of Hillend Fort, and even more convinced of the practicality of using the 3 by 1 grid diagonal, and indeed this particular grid. Found on Bornholm, applied to Scotland, and defining a specific, and very special point in the construct provided by William Buehler. Wow!
This third drawing is simple in comparison. It is the point which forms an equilateral triangle with the two base points.

Again using the half base length, 352.59 O.S units and the tangent of 60 degrees, defines the point on the axis:
Tan 60 * 352.59 = 610.70 O.S. units
x and y components found using the offset angle of 17.4742 degrees:
x: sin 17.4742 * 610.70 = 183.38 O.S. units
y: cos 17.4742 * 610.70 = 582.52 O.S. units
and again using base centre:
x: 3380.88 - 183.38 = 3197.50
y: 6233.87 + 582.52 = 6816.39
Oxcars (NT 202 817) a tiny island in the Forth is the nearest land, about 0.5 km, but the line clips Inchcolm at the eastern end, a distance of approx 0.75 km.
Friday 17 October 2008
St.Mary's Chapel grid, continued!
The set of graphics below show first what has been established previously, the first two, and then the extension of the inner smaller derived grid, in (1/sq.root two) relationship, using Blackness Castle, and the simple use of grid diagonals, (2 by 1) and (3 by 1) to find a remarkable system linked to the work of William S. Buehler, whose original work, the ''20 mile radius'' system centred on St. Mary's Chapel. The square on this circle, with The Bass Rock as north-east corner, and the subsidiary system oriented on North Berwick Law, and indeed another with Arther's' Seat summit as main North axis at the half-radius point, (which incidentally has Rosslyn Chapel on it, discussed previously) with a spread of approximately 2.5 degrees is shown in the first sketch.
Sketch One
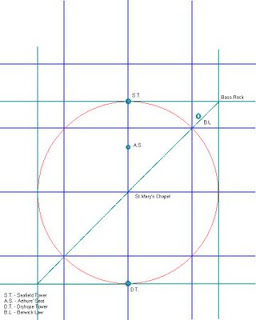
This shows the original circle and square grid derived from it, with a few points marked, St. Marys Chapel(NT275 570) in the centre, The Bass Rock(NT602 873) at the north-east corner, with North Berwick Law(NT556 842) indicated, Seafield(NT279 885) and Dryhope Towers(NT267 247) marking the north and south points respectively. The Arther's' Seat area is marked, and is at the half-radius point, but not indicated as such, but may be considered further, but later! The derived inner grid is found naturally in the geometry!
Sketch Two
This shows the smaller, inner grid, in (1/sq.root two) relationship, with Blackness Castle indicated at the north-west corner.

The length of side of this grid is where the Scot's measure system reveals the phi connection, discussed in previous post. Namely, (16* sq.root 3* 33) / (2* 37) equals 12.35842 miles(S), (half of which is 6.17921).
Incidentally, the discrepancy from phi exact is 6.5 feet, which is lost in the practical margins of error in my method. I work at all times with the limit in practice suggested as the optimum that medieval surveyors could achieve by known methods, by Professor Lind, in connection with the Bornholm work of Erling Haagensen and Henry Lincoln, in The Templar's Secret Island. This limit is 1 in 2000, or 99.95%, as discussed previously. 6.17921 mile(S) is 99.982% of 6.18034 miles(S).
The Scot's measure system I use is that defined by John Reid, 1683, in The Scot's Gard'ner, with the Scot's mile being in the ratio of 37 : 33 with the English/Imperial system. Inches and feet are common. Which raises many questions, not considered here!
Also, extreme accuracy that can be expected from O.S. maps is one metre, as explained to me by a professional cartographer friend, so any coordinates used here will be less than this. I would allow myself a discrepancy of up to ten metres. 6.5 feet is less than two metres (1.98 metres, to be precise)!
The issue of what accuracy the designers/surveyors worked to is not known, but the number of sites/points that are 'spot-on' indicates they got lucky very often.
I have been encouraged to allow for 'telluric'* off-set, and/or geographic/landscape practicalities in the past. I have allowed myself some leeway as at Blackness Castle(NT055 792), or Seafield Tower(NT280 885), where the exact geometric point is off the coast. I have also allowed the consideration of the 2.5 degree spread, and that these two points sit within this spread, as marker points. And, as at Arther's' Seat, the natural area of Holyrood Park, to be a 'unit-point-area', when considering such distances as the 200 mile plus spanning most of Scotland, and previously discussed.
* related to earth forces in some way! No further comment, for now!
These diagrams are simple representations of the geometry found so far.
Sketch Three
In late 1999 I moved to Selkirk to write up my findings till then. As previously mentioned I got connected to the Internet, made contact with William S. Buehler, and the geometry expanded, commensurate with my growing awareness of the landscape of the Tweed Valley and the countryside between Selkirk and Edinburgh. I was a member of the Sauniere Society at the time, and was privileged to hear Alistair Moffat discussing his book, Arthur And The Lost Kingdom, where my attention was drawn to Kelso, and the Roxburghe Castle area, east of Selkirk, where the Tweed and Teviot rivers meet.
On investigation I found that Kelso Abbey(NT727 339) was at the corner of the (2 by 1) grid point, south-east of St. Mary's Chapel:

A quick calculation here, to establish the accuracy of this. I am doing this from memory, and only using a list of O.S. coordinates, and re-doing the calculations as I go. And, I am aware that Kelso Abbey is not the exact point, as it is in the Schiehallion system described previously, but that a point closer to Roxburghe Castle(NT713 337) is the exact point. I shall first consider Kelso Abbey, to establish that we are in the right area:
3275.00 6570.19 St. Mary's Chapel
3728.87 6337.92 Kelso Abbey
--------- ----------
-453.87 232.27
Us usual using Pythagoras' Theorem, a grid unit distance of 509.85 hundreds of metres; which converts to 31.681 miles(E). Converting to Scots measure; using (33/37) gives 28.2557 miles(S).
What needs to be established is the approximation to the ( 2 by 1) diagonal which this distance represents, and the angle to O.S. grid:
We know that the side of the grid square is 12.38542 miles(S), (6.17921 * 2), and that the ( 2 by 1 ) diagonal is side times square root five, and the angle has a tangent of (1/2), or its complementary angle with a tangent of (2/1), which are 26.565 degrees, and 63.435 degrees respectively!
(6.17921 * 2) * square root five = 27.6343 miles(S). This is 0.6214 miles(S) short of Kelso Abbey!
The angle to O.S. grid has as tangent: (453.87/232.27) = 62.8987 degrees. or its complement to 90 degrees of 27.1013 degrees. This latter figure can be added to 90 to allow comparison with the north axis of orientation of the O.S. grid; 90 + 27.1013 = 117.1013. The exact angle for this vector should be (90 + 26.56505) 116.56505 degrees. The difference is 0.53625 degrees, well within the 2.5 degree spread discussed above!
Kelso Abbey could well be considered a marker point, for this grid!
I am content to leave this for now. Should anyone care to do some calculations for themselves I give a few more points around Roxburgh Castle, and also Floors Castle just to the north of Roxburgh Castle:
3716.82 6339.96 'hillock' east of Roxburgh Castle
3710.00 6335.22 'hillock' south of Roxburgh Castle
3713.04 6337.38 mean of two previous
3711.12 6346.62 Floors Castle
Sketch Four
In this part Ericstane Hill(NT059 122) shall be considered in relation to Kelso Abbey as marking the (3 by 1) diagonal south- west, and St. Mary's Chapel, as the (2 by 1) point south and west.
Ericstane Hill is north of Moffat between the A701, and the A74(M), with the 'Devil's Beef Tub' where stolen cattle were apparently penned in seclusion, in the valley to the north-east. It is the area where the Annan river rises, and close to the source of the Tweed. There is a Roman fortlet on its flank, with also the Eric Stane and monument.

3728.87 6337.92 Kelso Abbey
3059.81 6121.89 EricStane Hill(summit)
---------- ----------
669.06 216.03
By Pythagoras' theorem; 703.072 O.S.units(hundred metres); 43.68687 miles(E); 38.964 miles(S).
Now, the diagonal of a (3 by 1) rectangle is square root ten, so dividing we get 12.32132 miles(S), against the square unit side of 12.3584 miles(S), a difference of 0.03708 m(S), a discrepancy of 71.2 ells, or 73 yards, too short.
In real terms it is a discrepancy of 230 yards over the full distance, not great, not bad, good enough for immediate purposes.
The angle to O.S. grid is tangent (669.06/216.03), which gives an angle of 72.1055, and complement to 90 degrees of 17.8945.
The angle of the line from St. Mary's Chapel to Kelso Abbey, from above was found to be 27.1013 degrees.
Now, interestingly, the adjacent angles of a (2 by 1) and (3 by 1) is 45 degrees exactly; so 27.1013 plus 17.8945 equals 44.9958, 45 - 0.0042 degrees
As a check, Ericstane Hill can be compared to St. Mary's Chapel:
3275.00 6570.19 St. Mary's Chapel
3059.81 6121.89 EricStane Hill(summit)
---------- ----------
215.19 448.30
By Pythagoras' theorem 497.2722 O.S. grid units(hundred metres); or 30.899miles(E); or 27.5586 miles(S).
Dividing by square root five(the length of a (2 by 1) diagonal) gives 12.3246 miles(S), a discrepancy of 0.03381 miles(S) from grid square length, 12.3584 miles(S), some 65 ells, or 67 yards, short, similar in scale to the Kelso Abbey measure.
The angle to O.S grid is tangent (215.19/448.3) = 25.64163 degrees, which added to the St. Mary's Chapel - Kelso Abbey angle of 62.8987 degrees is 88.54 degrees, against the 90 degrees it should be. a shortfall of 1.46 degrees, well within the spread of 2.5 degrees, disussed above.
I could 'tweak' things a bit, and get the exact spots at both Kelso and Ericstane, and have done so previously, it's all in my notes somewhere, but for now I shall leave this, content in having established these two areas as containing the corners of the grid centred on St. Mary's Chapel discussed above.
Sketch Five
This sketch shows the next task, establishing the (3 by 1) axis through St. Mary's Chapel, from the mid-point of the Kelso - Ericstane line shown here:

Sketch One

This shows the original circle and square grid derived from it, with a few points marked, St. Marys Chapel(NT275 570) in the centre, The Bass Rock(NT602 873) at the north-east corner, with North Berwick Law(NT556 842) indicated, Seafield(NT279 885) and Dryhope Towers(NT267 247) marking the north and south points respectively. The Arther's' Seat area is marked, and is at the half-radius point, but not indicated as such, but may be considered further, but later! The derived inner grid is found naturally in the geometry!
Sketch Two
This shows the smaller, inner grid, in (1/sq.root two) relationship, with Blackness Castle indicated at the north-west corner.

The length of side of this grid is where the Scot's measure system reveals the phi connection, discussed in previous post. Namely, (16* sq.root 3* 33) / (2* 37) equals 12.35842 miles(S), (half of which is 6.17921).
Incidentally, the discrepancy from phi exact is 6.5 feet, which is lost in the practical margins of error in my method. I work at all times with the limit in practice suggested as the optimum that medieval surveyors could achieve by known methods, by Professor Lind, in connection with the Bornholm work of Erling Haagensen and Henry Lincoln, in The Templar's Secret Island. This limit is 1 in 2000, or 99.95%, as discussed previously. 6.17921 mile(S) is 99.982% of 6.18034 miles(S).
The Scot's measure system I use is that defined by John Reid, 1683, in The Scot's Gard'ner, with the Scot's mile being in the ratio of 37 : 33 with the English/Imperial system. Inches and feet are common. Which raises many questions, not considered here!
Also, extreme accuracy that can be expected from O.S. maps is one metre, as explained to me by a professional cartographer friend, so any coordinates used here will be less than this. I would allow myself a discrepancy of up to ten metres. 6.5 feet is less than two metres (1.98 metres, to be precise)!
The issue of what accuracy the designers/surveyors worked to is not known, but the number of sites/points that are 'spot-on' indicates they got lucky very often.
I have been encouraged to allow for 'telluric'* off-set, and/or geographic/landscape practicalities in the past. I have allowed myself some leeway as at Blackness Castle(NT055 792), or Seafield Tower(NT280 885), where the exact geometric point is off the coast. I have also allowed the consideration of the 2.5 degree spread, and that these two points sit within this spread, as marker points. And, as at Arther's' Seat, the natural area of Holyrood Park, to be a 'unit-point-area', when considering such distances as the 200 mile plus spanning most of Scotland, and previously discussed.
* related to earth forces in some way! No further comment, for now!
These diagrams are simple representations of the geometry found so far.
Sketch Three
In late 1999 I moved to Selkirk to write up my findings till then. As previously mentioned I got connected to the Internet, made contact with William S. Buehler, and the geometry expanded, commensurate with my growing awareness of the landscape of the Tweed Valley and the countryside between Selkirk and Edinburgh. I was a member of the Sauniere Society at the time, and was privileged to hear Alistair Moffat discussing his book, Arthur And The Lost Kingdom, where my attention was drawn to Kelso, and the Roxburghe Castle area, east of Selkirk, where the Tweed and Teviot rivers meet.
On investigation I found that Kelso Abbey(NT727 339) was at the corner of the (2 by 1) grid point, south-east of St. Mary's Chapel:

A quick calculation here, to establish the accuracy of this. I am doing this from memory, and only using a list of O.S. coordinates, and re-doing the calculations as I go. And, I am aware that Kelso Abbey is not the exact point, as it is in the Schiehallion system described previously, but that a point closer to Roxburghe Castle(NT713 337) is the exact point. I shall first consider Kelso Abbey, to establish that we are in the right area:
3275.00 6570.19 St. Mary's Chapel
3728.87 6337.92 Kelso Abbey
--------- ----------
-453.87 232.27
Us usual using Pythagoras' Theorem, a grid unit distance of 509.85 hundreds of metres; which converts to 31.681 miles(E). Converting to Scots measure; using (33/37) gives 28.2557 miles(S).
What needs to be established is the approximation to the ( 2 by 1) diagonal which this distance represents, and the angle to O.S. grid:
We know that the side of the grid square is 12.38542 miles(S), (6.17921 * 2), and that the ( 2 by 1 ) diagonal is side times square root five, and the angle has a tangent of (1/2), or its complementary angle with a tangent of (2/1), which are 26.565 degrees, and 63.435 degrees respectively!
(6.17921 * 2) * square root five = 27.6343 miles(S). This is 0.6214 miles(S) short of Kelso Abbey!
The angle to O.S. grid has as tangent: (453.87/232.27) = 62.8987 degrees. or its complement to 90 degrees of 27.1013 degrees. This latter figure can be added to 90 to allow comparison with the north axis of orientation of the O.S. grid; 90 + 27.1013 = 117.1013. The exact angle for this vector should be (90 + 26.56505) 116.56505 degrees. The difference is 0.53625 degrees, well within the 2.5 degree spread discussed above!
Kelso Abbey could well be considered a marker point, for this grid!
I am content to leave this for now. Should anyone care to do some calculations for themselves I give a few more points around Roxburgh Castle, and also Floors Castle just to the north of Roxburgh Castle:
3716.82 6339.96 'hillock' east of Roxburgh Castle
3710.00 6335.22 'hillock' south of Roxburgh Castle
3713.04 6337.38 mean of two previous
3711.12 6346.62 Floors Castle
Sketch Four
In this part Ericstane Hill(NT059 122) shall be considered in relation to Kelso Abbey as marking the (3 by 1) diagonal south- west, and St. Mary's Chapel, as the (2 by 1) point south and west.
Ericstane Hill is north of Moffat between the A701, and the A74(M), with the 'Devil's Beef Tub' where stolen cattle were apparently penned in seclusion, in the valley to the north-east. It is the area where the Annan river rises, and close to the source of the Tweed. There is a Roman fortlet on its flank, with also the Eric Stane and monument.

3728.87 6337.92 Kelso Abbey
3059.81 6121.89 EricStane Hill(summit)
---------- ----------
669.06 216.03
By Pythagoras' theorem; 703.072 O.S.units(hundred metres); 43.68687 miles(E); 38.964 miles(S).
Now, the diagonal of a (3 by 1) rectangle is square root ten, so dividing we get 12.32132 miles(S), against the square unit side of 12.3584 miles(S), a difference of 0.03708 m(S), a discrepancy of 71.2 ells, or 73 yards, too short.
In real terms it is a discrepancy of 230 yards over the full distance, not great, not bad, good enough for immediate purposes.
The angle to O.S. grid is tangent (669.06/216.03), which gives an angle of 72.1055, and complement to 90 degrees of 17.8945.
The angle of the line from St. Mary's Chapel to Kelso Abbey, from above was found to be 27.1013 degrees.
Now, interestingly, the adjacent angles of a (2 by 1) and (3 by 1) is 45 degrees exactly; so 27.1013 plus 17.8945 equals 44.9958, 45 - 0.0042 degrees
As a check, Ericstane Hill can be compared to St. Mary's Chapel:
3275.00 6570.19 St. Mary's Chapel
3059.81 6121.89 EricStane Hill(summit)
---------- ----------
215.19 448.30
By Pythagoras' theorem 497.2722 O.S. grid units(hundred metres); or 30.899miles(E); or 27.5586 miles(S).
Dividing by square root five(the length of a (2 by 1) diagonal) gives 12.3246 miles(S), a discrepancy of 0.03381 miles(S) from grid square length, 12.3584 miles(S), some 65 ells, or 67 yards, short, similar in scale to the Kelso Abbey measure.
The angle to O.S grid is tangent (215.19/448.3) = 25.64163 degrees, which added to the St. Mary's Chapel - Kelso Abbey angle of 62.8987 degrees is 88.54 degrees, against the 90 degrees it should be. a shortfall of 1.46 degrees, well within the spread of 2.5 degrees, disussed above.
I could 'tweak' things a bit, and get the exact spots at both Kelso and Ericstane, and have done so previously, it's all in my notes somewhere, but for now I shall leave this, content in having established these two areas as containing the corners of the grid centred on St. Mary's Chapel discussed above.
Sketch Five
This sketch shows the next task, establishing the (3 by 1) axis through St. Mary's Chapel, from the mid-point of the Kelso - Ericstane line shown here:

Friday 10 October 2008
St. Mary's Chapel, Mount Lothian grid contd.

So, having established That there is a grid in Lothian, based on the the exact same dimensions as that found at Bornholm, with St. Mary's Chapel and St. Baldred's Chapel on The Bass Rock forming the diagonal, which links with the side of a square through Dunsappie hill-fort and extends to Seafield Tower between Kinghorn and Kirkcaldy, I shall now show the other diagonal, north-west of St. Mary's Chapel. This diagonal can be fixed by Blackness Castle, and a natural sub-division is found, namely the side of the square fixed by Seafield Tower, becomes the diagonal of a smaller nested square, which shall then be used in the next quite astonishing development. For this exercise though, I shall use the North Berwick Law orientation, confirming that in the landscape, both are relevant. See below!
3275.00 6570.19 St. Mary's Chapel
3055.66 6792.48 Blackness Castle
---------- ----------
219.34 -222.29
Using Pythagoras' Theorem: 312.29 O.S grid units(100 metre), which converts to:
19.4046 miles(E), which is some 337 yards short of the exact figure of 19.596 miles(E)! Now as Blackness juts out into the Firth of Forth, the exact point is in fact off-shore, just like at Seafield Tower.

Through calculation the exact grid reference is found to be :
3275.00 6570.19 St. Mary's Chapel
3055.71 6796.88 Blackness(calculated point)
---------- ----------
319.29 -226.69
again, using Pythagoras' theorem: 315.40 grid units of 100 metres, which converts to: 19.598 miles(E), and allowing for the small rounding off in the calculations is good to 0.002 miles! (I have restricted the figures to two decimal places for convenience here, and to 3 decimal places in the final miles calculation! A discrepancy of some 10 feet. I trust this is acceptable! I normally work to 10 figures on the calculator!)
And the angle to grid north is 44.05 degrees west of grid north, which corresponds to ninety degrees difference to the North Berwick line, 45.95 degrees east of grid north.
The grid squares having diagonal St.Mary's Chapel to Blackness are shown below, with sides equal to 19.598 miles(E)/square root 2 = 13.858 miles(E):

The next section uses this smaller square as the grid unit for the next stage, which extends this grid in all directions.
Now, a final point for now, as I have just realized:
This grid square side length of 13.858 miles(E) is equal to 12.36 miles(S)(33/37 is the onversion factor, see explanation in previous posts, and why I here, always distinguish between the two systems by the (E) and (S).
Now, half of 12.36 miles(S) is 6.18, a harmonic of phi, or little phi, or 1/Phi!!!
This is a new finding, although I may have it in my notes, but I don't recall having found this previously in relation to this system, and has to be of significance, to my mind! Quite astonishing, but then again, that's nothing new in this whole research!
I shall work on this, and see what else is to be found!
Good grief, the time on my computer at this exact moment is 6.19am, BST!!!
I had just done some calculations, one of the dogs barked, and I checked the clock!!!!
This is what I found:
The Bornholm grid axis is 16*square root three miles(E). This equates to 24.71683315miles(S). This divided by 40 gives 0.617920828. The reciprocal is 1.6183303, which squared is 2.61899296. Now that is an approximation of Phisquared, or Phi^2. This multiplied by 6/5; or 1.2 is 3.142791552, which multiplied by 7 = 21.99954086, which is 99.998% of 22. 22/7 is a rough, and often used form of Pi.
So, this grid, and hence the Bornholm grid, in Scottish measure is based on a common form of Pi, and Phi! I had found some correlation with Scottish measure when I was working on the Bornholm grid, but nothing so convincing!
So the full factors involved must all resolve in some way:
[(16*sq.rt3*33/37*40)^2]*5/6 = 7/22; so; (16^2,*3,*33^2,*5,*22)/(37^2,*40^2,*7) = 1;
which resolves to (2^2,*3^2,*11^3)/(5,*37^2) = 47916/47915; which equals 1.00002087, the reciprocal of which is 0.99997913, equivalent to 99.9979% of 1.
Interesting exercise! Or perhaps I should get a life!?
Then again, astonishing find!
Thursday 2 October 2008
St.Mary's Chapel Bass Rock system further consideration
Having established the Bass Rock line, and considering this to be the diagonal of a square, the vertical will be 45 degrees anti-clockwise, a line which proves to run through the Arthurs' Seat area, and in fact a special rock on Dunsappie Fort, which I call pulpit Rock, whih intrigued me when first found back in the mid-nineties. The line extended north finishes just east of Seafield Tower, just offshore.



A lot of calculations were done using both the Bass Rock and North Berwick Law alignments, but the easiest way here is to just show the Dunsappie calculations first then the Seafield Tower point, just to keep things simple:
3275.00 6570.19 St. Mary's Chapel
3281.32 6731.72 Dunsappie 'notch' or Pulpit Rock
---------- ----------
-6.32 -161.53
Using Pythagoras again the distance is 161.6536, in One hundred metre units which converts to 10.0447 miles(E). This may be of interest but for now it is the angle this line makes to the O.S grid for comparison to the Bass Rock line:
6.32/161.53 = 0.039126, which is the tangent of 2.2406 degrees.
Comparing to the Bass Rock angle of 47.1803 - 2.2406 = 44.94 degrees, which is 0.06 degrees, or 1/100th of one clock-face-minute!
As the diagonal of a square is in square root two relationship with the side, this line extended north to a distance of 19.59592 miles(E), (16*sq.rt.3/sq.rt.2), the point indicated on the map just off-shore at Seafield Tower, which lies between Kinghorn and Kirkcaldy, is found.
Now that the St.Mary's -Bass Rock-Seafield Tower 45 degree right-angled triangle has been established, the full square can be projected, to complete the square on the circle of Bill Buehler's original circular system. And also, some of the sub-divisions also show points of interest.

click on image to see larger version!
This schematic was drawn prior to the calculations, and was what I needed to verify. It is good enough for now, as it shows the extended square and circle and some natural sub-divisions.
AS stand for Arthurs' Seat, and can be seen to be halfway between St. Mary's Chapel and Seafield Tower. It should be pointed out that the exact halfway point is some 440 yards south of Dunsappie, or one quarter mile, which is Duddingston loch, a beautiful spot famed in Scottish art for the painting by Raeburn of the Reverend Walker skating on Duddingston loch. And on the north-east shore lies Duddingston Kirk, the minister at the time was the Reverend John Thomson, who was also an amateur painter and had a studio down by the shore, still extant, an octagonal building which was also the home of the first curling club in the world.
Intriguingly, on the north wall of the kirk is a carved symbol, the same as is shown in 'The Templars' Secret Island', the book of the geometry of Bornholm, by Erling Haaagensen and Henry Lincoln, page 13, where there are examples of stones from Bodilsker, Nylars, Osterlars and Vestermarie, which 'echo the Cross of the Knights Templar'.


It should also be pointed out that there is also the Line from St. Mary's Chapel through Rosslyn Chapel and Arthurs' Seat summit which is the Roseline commonly or as Bill Buehler calls it the Tavhara Line, which passes just to the west of Seafield Tower, previously mentioned. This may constitute a more generous Selah Spoke, with the North Berwick Law line running between Arthurs' Seat and Dunsappie, and we can in passing check this:
3275.00 6570.19 St. Mary's Chapel
3275.28 6729.43 Arthurs' Seat summit
---------- ----------
-0.28 -159.24
and using Pythagoras' theorem: 159.24 O.S.units of 100 meters, which equates to 9.895 miles(E), and the angle to O.S. grid north being: 0.28/159.24 = 0.00176, which is the tangent of 0.1 degrees.
So the gap between this line and the Dunsappie line being 2.24 - 0.1 = 2.14 degrees, which may be considered as a 'Selah spoke'!
I consider the Arthurs' Seat area to be a 'unit point area' at large landscape scale.
So this gap being contained within the Arthurs' Seat area at a landscape scale this may be considered valid!
Also, and more pertinent to the next section is the Blackness Castle/Drem line. This can be seen to be between the diagonals at a distance the same as Seafield Tower, taken as radius. The squares on these sections of diagonals prove to be the unit squares of the next sub-system to be described! See next section!



A lot of calculations were done using both the Bass Rock and North Berwick Law alignments, but the easiest way here is to just show the Dunsappie calculations first then the Seafield Tower point, just to keep things simple:
3275.00 6570.19 St. Mary's Chapel
3281.32 6731.72 Dunsappie 'notch' or Pulpit Rock
---------- ----------
-6.32 -161.53
Using Pythagoras again the distance is 161.6536, in One hundred metre units which converts to 10.0447 miles(E). This may be of interest but for now it is the angle this line makes to the O.S grid for comparison to the Bass Rock line:
6.32/161.53 = 0.039126, which is the tangent of 2.2406 degrees.
Comparing to the Bass Rock angle of 47.1803 - 2.2406 = 44.94 degrees, which is 0.06 degrees, or 1/100th of one clock-face-minute!
As the diagonal of a square is in square root two relationship with the side, this line extended north to a distance of 19.59592 miles(E), (16*sq.rt.3/sq.rt.2), the point indicated on the map just off-shore at Seafield Tower, which lies between Kinghorn and Kirkcaldy, is found.
Now that the St.Mary's -Bass Rock-Seafield Tower 45 degree right-angled triangle has been established, the full square can be projected, to complete the square on the circle of Bill Buehler's original circular system. And also, some of the sub-divisions also show points of interest.

click on image to see larger version!
This schematic was drawn prior to the calculations, and was what I needed to verify. It is good enough for now, as it shows the extended square and circle and some natural sub-divisions.
AS stand for Arthurs' Seat, and can be seen to be halfway between St. Mary's Chapel and Seafield Tower. It should be pointed out that the exact halfway point is some 440 yards south of Dunsappie, or one quarter mile, which is Duddingston loch, a beautiful spot famed in Scottish art for the painting by Raeburn of the Reverend Walker skating on Duddingston loch. And on the north-east shore lies Duddingston Kirk, the minister at the time was the Reverend John Thomson, who was also an amateur painter and had a studio down by the shore, still extant, an octagonal building which was also the home of the first curling club in the world.
Intriguingly, on the north wall of the kirk is a carved symbol, the same as is shown in 'The Templars' Secret Island', the book of the geometry of Bornholm, by Erling Haaagensen and Henry Lincoln, page 13, where there are examples of stones from Bodilsker, Nylars, Osterlars and Vestermarie, which 'echo the Cross of the Knights Templar'.


It should also be pointed out that there is also the Line from St. Mary's Chapel through Rosslyn Chapel and Arthurs' Seat summit which is the Roseline commonly or as Bill Buehler calls it the Tavhara Line, which passes just to the west of Seafield Tower, previously mentioned. This may constitute a more generous Selah Spoke, with the North Berwick Law line running between Arthurs' Seat and Dunsappie, and we can in passing check this:
3275.00 6570.19 St. Mary's Chapel
3275.28 6729.43 Arthurs' Seat summit
---------- ----------
-0.28 -159.24
and using Pythagoras' theorem: 159.24 O.S.units of 100 meters, which equates to 9.895 miles(E), and the angle to O.S. grid north being: 0.28/159.24 = 0.00176, which is the tangent of 0.1 degrees.
So the gap between this line and the Dunsappie line being 2.24 - 0.1 = 2.14 degrees, which may be considered as a 'Selah spoke'!
I consider the Arthurs' Seat area to be a 'unit point area' at large landscape scale.
So this gap being contained within the Arthurs' Seat area at a landscape scale this may be considered valid!
Also, and more pertinent to the next section is the Blackness Castle/Drem line. This can be seen to be between the diagonals at a distance the same as Seafield Tower, taken as radius. The squares on these sections of diagonals prove to be the unit squares of the next sub-system to be described! See next section!
Friday 29 August 2008
Bornholm Grid Part Two - Lothian Scotland
In this section, The grid, based on 16*sq.root three miles(E), found on Bornholm is confirmed with the very first calculation applied to Scotland. In 1999, I first made contact with Bill Buehler, an Earth-Grid researcher of some 30 plus years, and promoter of what is known as Reshel grid dynamics, and much more, (of which more later!). I had known of his Rosslyn Chapel geometric analysis, from two A4 photocopies that were lying in the shop at the Chapel, a couple of years previously. I don't know why there were two piles of these on a shelf opposite the counter, and the assistant/volunteer gave the ok to take a copy of each, presumably there for use by a tour party. One was a plan of the Chapel, and the other an elevation, both with complex geometric constructs, and labeled with terms totally foreign to me, with explanations mostly beyond my comprehension, seeming to hint at a life spirit/force based on principles of geometric design, which the Chapel Design seemed to follow perfectly. It was the first hint that the geometry I had been finding, was somehow more precisely purposed than a mere cartographic exercise. I had ound of course precise pentagonal geometry, which did in fact incorporate Rosslyn Chapel, and related in measure to what Henry Lincoln had described in the south of France. More on this later!
When I had joined a discussion forum there was a topic in which this same mysterious terminology was referred to, so I posted my interest, and described something of what I had found. Biil Buehler answered, explaining that what I had obtained in the Chapel Tea-Room was his work. He congratulated me on my work, very pleased with the pentagonal system I had found, and even more so when I described a feature in the landscape, which I still have to describe, which for him was a sure sign of activation of a Reshel Grid system in the Edinburgh/Rosslyn area. I have been receiving posts from Bill for some Nine years now, and there have been many fascinating developments in that time.
One of the first systems he described in the landscape was based on the Roseline, or in Bill's terminology the Tavhara line, which passed through Arthurs' Seat Summit, Rosslyn Chapel, and St. Mary's Chapel to the south at Mount Lothian. This line I knew of, it's the one everyone finds. Bill described though a Reshel system, centred on St. Mary's Chapel, and a 20 mile radius circle, from Seafield Tower in the north, between Kinghorn and Kirkcaldy, in Fife, and Dryhope Tower in the Yarrow valley, near St. Mary's Loch to the south.

copyright William S. Buehler
It is the recti-linear grid derived from this graphic that I had been working on for a few years, finding The Bass Rock to be at the north east corner of the square constructed on the 40 mile diameter outer circle. This was one of the main systems that had developed when I had moved to Selkirk in the Scottish Borders, and the geometry kind of opened up or expanded with my investigations of the landscape, as I commuted back and forth to Edinburgh. I shall expand on this later.
After my Bornholm exercise, it was the diagonal from St. Mary's to The Bass Rock, I wanted to try first. I obtained the two relevant sections of 1:25,000 O.S. maps from the 'Get-A-Map' feature on their website, from the local library. And the obvious place to try on The Bass, was St. Baldred's Chapel. I worked out the grid references to the metre for both points, and did the calculations. To my total amazement, it was to within a few feet 16*Square root three miles (E), the exact same as the grid found on Bornholm.
Deleted google map, for now, see top of page!
The three main lines for now are the St.M's to The Bass Rock, St. M's to N. Berwick Law, and the St.M's to Dunsappie extended line.
Monday 22 Sept, 2998, equinox!
OK, after a few weeks break, I should get back to work!
Calculations
1. St. Mary's Chapel, Mount Lothian, (NT 275 570) to St. Baldred's Chapel, The Bass Rock. (NT 602 873).
3275.00 6570.19 St Mary's Chapel
3602.26 6873.26 St. Baldred's Chapel
---------- ----------
-327.26 -303.07
Using Pythagoras Theorem: 446.04 0.S.grid units of 100metres
which converts to 27.71556 miles (E)
divided by sq.root three = 16.0016, which is a 99.99% correlation with 16!
I am redoing the calculations as I go, with my hand-held calculator, as a check, and this still amazes me, how close it is to the Bornholm grid size. It is 8.4 feet and the references are calculated to the metre, 3.28084 feet, in theory only, in practice my calculations involve small areas of map, and pencil and ruler, so there is an added discrepancy inherent.
The angle of this line to the O.S map can be compared to the others and the angles to each other compared!
Using the two calculated figures above to give the tangent ratio the angle can be obtained.
(-327.06)/(-303.07) = 1.07915663, this gives the angle as 47.1802838.
The North Berwick Law line from St.Mary's Chapel, Mount Lothian
OK, time again to do some more. It is now Obtober first, another month of distraction and laziness.
Having established the Bass Rock line to St. Baldred's Chapel as being the exact same as the Bornholm grid, I need to show another possibility, on a slightly diferent orientation. This time using North Berwick Law:
3275.00 6570.19 St Mary's Chapel
3556.32 6842.23 N. Berwick Law
---------- ----------
-281.32 -272.04
again using Pythagoras' theorem: 391.34 O.S.grid units of 100 metres
which converts to 24.31672 miles(E)
which divided by square root three, gives 14.0393, which is a 99.72% correlation with 14. This discrepancy is some 69 yards, so not to the same 'exactness' as I normally allow, but North Berwick Law and The Bass Rock do seem to interact in the landscape from the area of Midlothian in the landscape.
The angle to O.S. grid again is found rom the tangent ratio of the two calculated components.
281.32/272.04 = 1.034113, which gives the angle 45.96 degrees.
I note this alignment due to the fact that Nylars Church on Bornholm marks the 13/16 point on the grid axis.
Compared to the Bass Rock line of 47.18 - 45.96 = 1.22 degrees, or 'roughly' one fifth of one clock-face-minute!(one c.f.m. is six degrees, there being 60 minutes in one hour, or 360 degrees!)
This could be considered as a 'Selah-spoke' in Bill Buehler's terminology, which he normally expects in a 'spinner' system. In discussion he would actually want it a bit greater, up to 3 degrees. I shall from here on consider only the Bass Rock alignment, but it should be kept in mind that this second alignment is there.
When I had joined a discussion forum there was a topic in which this same mysterious terminology was referred to, so I posted my interest, and described something of what I had found. Biil Buehler answered, explaining that what I had obtained in the Chapel Tea-Room was his work. He congratulated me on my work, very pleased with the pentagonal system I had found, and even more so when I described a feature in the landscape, which I still have to describe, which for him was a sure sign of activation of a Reshel Grid system in the Edinburgh/Rosslyn area. I have been receiving posts from Bill for some Nine years now, and there have been many fascinating developments in that time.
One of the first systems he described in the landscape was based on the Roseline, or in Bill's terminology the Tavhara line, which passed through Arthurs' Seat Summit, Rosslyn Chapel, and St. Mary's Chapel to the south at Mount Lothian. This line I knew of, it's the one everyone finds. Bill described though a Reshel system, centred on St. Mary's Chapel, and a 20 mile radius circle, from Seafield Tower in the north, between Kinghorn and Kirkcaldy, in Fife, and Dryhope Tower in the Yarrow valley, near St. Mary's Loch to the south.

copyright William S. Buehler
It is the recti-linear grid derived from this graphic that I had been working on for a few years, finding The Bass Rock to be at the north east corner of the square constructed on the 40 mile diameter outer circle. This was one of the main systems that had developed when I had moved to Selkirk in the Scottish Borders, and the geometry kind of opened up or expanded with my investigations of the landscape, as I commuted back and forth to Edinburgh. I shall expand on this later.
After my Bornholm exercise, it was the diagonal from St. Mary's to The Bass Rock, I wanted to try first. I obtained the two relevant sections of 1:25,000 O.S. maps from the 'Get-A-Map' feature on their website, from the local library. And the obvious place to try on The Bass, was St. Baldred's Chapel. I worked out the grid references to the metre for both points, and did the calculations. To my total amazement, it was to within a few feet 16*Square root three miles (E), the exact same as the grid found on Bornholm.
Deleted google map, for now, see top of page!
The three main lines for now are the St.M's to The Bass Rock, St. M's to N. Berwick Law, and the St.M's to Dunsappie extended line.
Monday 22 Sept, 2998, equinox!
OK, after a few weeks break, I should get back to work!
Calculations
1. St. Mary's Chapel, Mount Lothian, (NT 275 570) to St. Baldred's Chapel, The Bass Rock. (NT 602 873).
3275.00 6570.19 St Mary's Chapel
3602.26 6873.26 St. Baldred's Chapel
---------- ----------
-327.26 -303.07
Using Pythagoras Theorem: 446.04 0.S.grid units of 100metres
which converts to 27.71556 miles (E)
divided by sq.root three = 16.0016, which is a 99.99% correlation with 16!
I am redoing the calculations as I go, with my hand-held calculator, as a check, and this still amazes me, how close it is to the Bornholm grid size. It is 8.4 feet and the references are calculated to the metre, 3.28084 feet, in theory only, in practice my calculations involve small areas of map, and pencil and ruler, so there is an added discrepancy inherent.
The angle of this line to the O.S map can be compared to the others and the angles to each other compared!
Using the two calculated figures above to give the tangent ratio the angle can be obtained.
(-327.06)/(-303.07) = 1.07915663, this gives the angle as 47.1802838.
The North Berwick Law line from St.Mary's Chapel, Mount Lothian
OK, time again to do some more. It is now Obtober first, another month of distraction and laziness.
Having established the Bass Rock line to St. Baldred's Chapel as being the exact same as the Bornholm grid, I need to show another possibility, on a slightly diferent orientation. This time using North Berwick Law:
3275.00 6570.19 St Mary's Chapel
3556.32 6842.23 N. Berwick Law
---------- ----------
-281.32 -272.04
again using Pythagoras' theorem: 391.34 O.S.grid units of 100 metres
which converts to 24.31672 miles(E)
which divided by square root three, gives 14.0393, which is a 99.72% correlation with 14. This discrepancy is some 69 yards, so not to the same 'exactness' as I normally allow, but North Berwick Law and The Bass Rock do seem to interact in the landscape from the area of Midlothian in the landscape.
The angle to O.S. grid again is found rom the tangent ratio of the two calculated components.
281.32/272.04 = 1.034113, which gives the angle 45.96 degrees.
I note this alignment due to the fact that Nylars Church on Bornholm marks the 13/16 point on the grid axis.
Compared to the Bass Rock line of 47.18 - 45.96 = 1.22 degrees, or 'roughly' one fifth of one clock-face-minute!(one c.f.m. is six degrees, there being 60 minutes in one hour, or 360 degrees!)
This could be considered as a 'Selah-spoke' in Bill Buehler's terminology, which he normally expects in a 'spinner' system. In discussion he would actually want it a bit greater, up to 3 degrees. I shall from here on consider only the Bass Rock alignment, but it should be kept in mind that this second alignment is there.
Tuesday 22 July 2008
Bornholm Island, Baltic Sea, grid findings. Part One.
Introduction
This section summarizes the main results of many months of calculations on the data supplied by the Danish Government mapping office, Kort & Matrikelstyrelsen System 45 Bornholm, as provided by Erling Haagensen and Henry Lincoln in 'The Templars' Secret Island', page 177, published in the year 2000.
I restrict the findings to what is most relevant to the landscape geometry of the Lothians and Border regions of Scotland.
For this purpose I require only to use three site coordinates, those of Point Christianso*, where it is believed that a compass rose was carved in the bedrock of the small island, some 12 miles north-east of Bornholm, and two of the four round churches on the actual island of Bornholm, Osterlars* and Nylars. A fourth found/calculated point, at sea, is also used, and labeled by the authors Point C.
(* there should be a diagonal stroke through the 'O' of Osterlars, and the small case 'o' at the end of Christianso. Apologies if the omission offends, I don't have the correct characters to hand.)
The coordinates given here are the theoretical coordinates calculated by Haagensen and Lincoln, based on the altars to the east of both churches and the calculated position of the compass rose, which was blown up for building material at the end of the 17th century, and is mentioned in an extant letter by the officer in charge of the defensive construction at the time.
The actual Kort & Matrikelstyrelsen coordinates are for the tips of the conical roofs of the two circular churches. to the west of the altars, and for the Store Tarn on Christianso.
Haagensen's calculations were 'checked' by Distinguished Professor Emeritus Niels C. Lind at the University of Waterloo, Victoria, BC. His letter of reply is on page 144.
His first point of consideration was the accuracy of Haagensen's calculations:
(1) I calculated the coordinates of 12 churches and four auxiliary points according to the layout you specify in your Appendix, using a double precision computer spreadsheet. I have not discovered any errors in your calculations.**
(Neither did I, and took that as in some way verifying my methods, and workings. TG)
**My italics and bold. Lind merely has the final statement in italics!
This is in essence all that is necessary for the main point under discussion here. His fourth point I quote as it also gives a rule of thumb margin I use for accuracy of all the geometry I show in this blog. Namely 1:2000, or 99.95% accuracy:
(4)It is interesting to consider how medieval surveyors could have laid out a design such as ''the map'' in the field and positioned the churches. I have several years experience with similar field work, albeit using mid-20th century technology. I have no knowledge of what instruments and procedures they can have used, but they probably laid out open traverses in the terrain, sighting by eye and chaining distances with metal chains without correcting for temperature, sag and slope. I believe they could not achieve accuracies better than 1:2000 in the measured lengths over 10-20 km distances in fairly wooded and hilly terrain and 0.01 degree in directions. This would give RMS* errors of at least 7 m, roughly. Again, my italics - TG!
* RMS I take to mean Root Mean Square, of which I am not accustomed to using, and take his word on this final statement which he gives in italics which I also em-bold-en:
An RMS error of about 24.8 m, as found in (2) above** is not incompatible with the belief that the churches were located according to a plan such as ''the map''.
** not included here!
This letter is dated March 22, 1999.
Their book was published in 2000, and I was lucky enough to be at the launch at the Sauniere Symposium at Newbattle, in Midlothian, Scotland. I knew then I would have to study the material. It is now 2008 and am only getting to the stage of presenting it all! Time, continuous new findings, reading, computer resources/skills and so on.
I did my work on this in 2003/4, and wrote a report dated 10th November 2004, and distributed to a few friends/associates, along with an additional report covering the follow-up investigation into the landscape geometry of Scotland on 16th December, 2004.
Calculations
Keeping this section as simple as possible, the first and most important point to show is the span of the grid which follows by implication, namely the distance between the two furthest points on the line, from the island of Christianso through Osterlars and Nylars on Bornholm to the Point C, found by Haagensen and Lincoln:
the theoretical coordinatesin metres:
Y-component..... X-component
73,240.92 ............31,071.52 .........Point Christianso
39,444.21 ............60,223.48 .........Point C
------------ ............------------
33796.71 ............-29151.96
distance, by Pythagoras = 44632.44 metres
=146431.88 feet;
=27.7333 miles(E)
This distance is very close to 16*sq.root3, or27.7128 miles(E), a correspondence of 99.926%, or 0.0205 miles, or 108.24 feet, or 36 yards, over a distance of 27.7+miles(E).
This is all that is necessary for the next section when this 16*sq.rt.3 miles(E) is applied to a specific system in Scotland, namely St. Mary's Chapel in Midlothian to St.Baldred's Chapel on the Bass Rock in the Firth of Forth, near North Berwick.
I first came upon the 16*square root three miles(E)unit whilst doing the Christianso - Nylars distance:
Y-component..... X-component
73,240.92 ............31,071.52 .........Point Christianso
45,803.24.............54,738.38...........Nylars
-------------.............-------------
27,437.68.............-23,666.86
By Pythagoras' theorem: 36,234.604 metres, which converts to; 118,888 feet, or; 22.51514 miles(E), which divided by 'square root three' is 12.999122, which is a 99.99325% correspondence to 13.
And this also correlates to the system in Scotland, and complicates things somewhat as it indicates a second grid a mere degree or so off the main one, St. Baldred's Chapel/Bass Rock version mentioned above, but the second version using North Berwick Law at 14/16ths units of grid measure, as I shall cover in part two! Both systems centred on St. Mary's Chapel, Mount Lothian.
[I would like to include a bit on the Osterlars - Nylars measurement, which is on the same axis, and identified as the controlling radius of the system described by Haagensen and Lincoln.
y - coordinate..... x - coordinate
56,658.79............45,374.73..........Osterlars
45,803.24............54,738.38..........Nylars
-------------............-------------
10,855.55............-9,363.65
which is, by Pythagoras' theorem; 14,336 metres precisely(to within 4/100ths of a millimetre)!
For now I just wish to note that this radius gives a circle circumference of 56 miles(E) to 99.9875%, using pi - 22/7, and 99.945% using calculator pi, as indeed pointed out by (H & L).
There are some points of note which are interesting in themselves regarding this measure and the full grid measure, but not necessary for the immediate concern, applying the '16*square root three' miles(E) to the landscape of Scotland, centred on St. Mary's Chapel, Mount Lothian.]
A Google Map of Bornholm and main points. Osterlars and Nylars define the orientation, and Olsker Nyker extended defines Point C and meets axis at 30 degrees, hinting at hexagonal geometry.
The axis from Point C to Christianso is divided into 16 sections, each of 1.732 miles(E), (or the square root three):
View Larger Map
This section summarizes the main results of many months of calculations on the data supplied by the Danish Government mapping office, Kort & Matrikelstyrelsen System 45 Bornholm, as provided by Erling Haagensen and Henry Lincoln in 'The Templars' Secret Island', page 177, published in the year 2000.
I restrict the findings to what is most relevant to the landscape geometry of the Lothians and Border regions of Scotland.
For this purpose I require only to use three site coordinates, those of Point Christianso*, where it is believed that a compass rose was carved in the bedrock of the small island, some 12 miles north-east of Bornholm, and two of the four round churches on the actual island of Bornholm, Osterlars* and Nylars. A fourth found/calculated point, at sea, is also used, and labeled by the authors Point C.
(* there should be a diagonal stroke through the 'O' of Osterlars, and the small case 'o' at the end of Christianso. Apologies if the omission offends, I don't have the correct characters to hand.)
The coordinates given here are the theoretical coordinates calculated by Haagensen and Lincoln, based on the altars to the east of both churches and the calculated position of the compass rose, which was blown up for building material at the end of the 17th century, and is mentioned in an extant letter by the officer in charge of the defensive construction at the time.
The actual Kort & Matrikelstyrelsen coordinates are for the tips of the conical roofs of the two circular churches. to the west of the altars, and for the Store Tarn on Christianso.
Haagensen's calculations were 'checked' by Distinguished Professor Emeritus Niels C. Lind at the University of Waterloo, Victoria, BC. His letter of reply is on page 144.
His first point of consideration was the accuracy of Haagensen's calculations:
(1) I calculated the coordinates of 12 churches and four auxiliary points according to the layout you specify in your Appendix, using a double precision computer spreadsheet. I have not discovered any errors in your calculations.**
(Neither did I, and took that as in some way verifying my methods, and workings. TG)
**My italics and bold. Lind merely has the final statement in italics!
This is in essence all that is necessary for the main point under discussion here. His fourth point I quote as it also gives a rule of thumb margin I use for accuracy of all the geometry I show in this blog. Namely 1:2000, or 99.95% accuracy:
(4)It is interesting to consider how medieval surveyors could have laid out a design such as ''the map'' in the field and positioned the churches. I have several years experience with similar field work, albeit using mid-20th century technology. I have no knowledge of what instruments and procedures they can have used, but they probably laid out open traverses in the terrain, sighting by eye and chaining distances with metal chains without correcting for temperature, sag and slope. I believe they could not achieve accuracies better than 1:2000 in the measured lengths over 10-20 km distances in fairly wooded and hilly terrain and 0.01 degree in directions. This would give RMS* errors of at least 7 m, roughly. Again, my italics - TG!
* RMS I take to mean Root Mean Square, of which I am not accustomed to using, and take his word on this final statement which he gives in italics which I also em-bold-en:
An RMS error of about 24.8 m, as found in (2) above** is not incompatible with the belief that the churches were located according to a plan such as ''the map''.
** not included here!
This letter is dated March 22, 1999.
Their book was published in 2000, and I was lucky enough to be at the launch at the Sauniere Symposium at Newbattle, in Midlothian, Scotland. I knew then I would have to study the material. It is now 2008 and am only getting to the stage of presenting it all! Time, continuous new findings, reading, computer resources/skills and so on.
I did my work on this in 2003/4, and wrote a report dated 10th November 2004, and distributed to a few friends/associates, along with an additional report covering the follow-up investigation into the landscape geometry of Scotland on 16th December, 2004.
Calculations
Keeping this section as simple as possible, the first and most important point to show is the span of the grid which follows by implication, namely the distance between the two furthest points on the line, from the island of Christianso through Osterlars and Nylars on Bornholm to the Point C, found by Haagensen and Lincoln:
the theoretical coordinatesin metres:
Y-component..... X-component
73,240.92 ............31,071.52 .........Point Christianso
39,444.21 ............60,223.48 .........Point C
------------ ............------------
33796.71 ............-29151.96
distance, by Pythagoras = 44632.44 metres
=146431.88 feet;
=27.7333 miles(E)
This distance is very close to 16*sq.root3, or27.7128 miles(E), a correspondence of 99.926%, or 0.0205 miles, or 108.24 feet, or 36 yards, over a distance of 27.7+miles(E).
This is all that is necessary for the next section when this 16*sq.rt.3 miles(E) is applied to a specific system in Scotland, namely St. Mary's Chapel in Midlothian to St.Baldred's Chapel on the Bass Rock in the Firth of Forth, near North Berwick.
I first came upon the 16*square root three miles(E)unit whilst doing the Christianso - Nylars distance:
Y-component..... X-component
73,240.92 ............31,071.52 .........Point Christianso
45,803.24.............54,738.38...........Nylars
-------------.............-------------
27,437.68.............-23,666.86
By Pythagoras' theorem: 36,234.604 metres, which converts to; 118,888 feet, or; 22.51514 miles(E), which divided by 'square root three' is 12.999122, which is a 99.99325% correspondence to 13.
And this also correlates to the system in Scotland, and complicates things somewhat as it indicates a second grid a mere degree or so off the main one, St. Baldred's Chapel/Bass Rock version mentioned above, but the second version using North Berwick Law at 14/16ths units of grid measure, as I shall cover in part two! Both systems centred on St. Mary's Chapel, Mount Lothian.
[I would like to include a bit on the Osterlars - Nylars measurement, which is on the same axis, and identified as the controlling radius of the system described by Haagensen and Lincoln.
y - coordinate..... x - coordinate
56,658.79............45,374.73..........Osterlars
45,803.24............54,738.38..........Nylars
-------------............-------------
10,855.55............-9,363.65
which is, by Pythagoras' theorem; 14,336 metres precisely(to within 4/100ths of a millimetre)!
For now I just wish to note that this radius gives a circle circumference of 56 miles(E) to 99.9875%, using pi - 22/7, and 99.945% using calculator pi, as indeed pointed out by (H & L).
There are some points of note which are interesting in themselves regarding this measure and the full grid measure, but not necessary for the immediate concern, applying the '16*square root three' miles(E) to the landscape of Scotland, centred on St. Mary's Chapel, Mount Lothian.]
A Google Map of Bornholm and main points. Osterlars and Nylars define the orientation, and Olsker Nyker extended defines Point C and meets axis at 30 degrees, hinting at hexagonal geometry.
The axis from Point C to Christianso is divided into 16 sections, each of 1.732 miles(E), (or the square root three):
View Larger Map
Thursday 10 July 2008
Tinto Hill - Preston Cross - Isle of May
Having had a break of some weeks from the geometry, I was checking a sketch I had done a few years back, and noticed a line I had not checked by calculation. It passes again through the unicorn Cross at Preston(NT 391 740), and links two points not previously mentioned, Tinto Hill(NS 952 343) and the Isle of May, or May Isle(NT 658 990, which is the Grid Reference for St. Adrian's Chapel).
[When I started my investigation, I was working with 1:25,000 scale maps, and the Isle of May was too far north of Lothian, as was Fife, and so no casual links could be made. The same was true for Tinto Hill, but to the south. It was when I was living in Selkirk that Tinto came to my awareness, as the part of a grid I shall be describing soon.]
The full grid references I shall use:
2952.75 6343.79 Tinto Hill
2965.23 6345.47 Scout Hill, a hill a mile to the east of Tinto, which is found to be a more exact point in line with the southern point on The May Isle.
3391.27 6740.57 Preston Cross, {unicorn}
3658.68 6990.19 St. Adrian's Chapel, May Isle.
3662.83 6988.49 South Ness, May Isle.
3658.68 6990.19 May Isle, St. Adrian's Chapel. The May Isle is roughly at 45 degrees to grid, from North-west to south-east and is a bit more than the diagonal of a grid kilometre square, or a mile approximately. The range is from North Ness {NT 651 999} to South Ness (NT 662 988}.
Marked features on the Island include, between St.Adrian's Chapel and South Ness, Pilgrim's Haven, Pilgrim's Well, Maiden Hair, The Pillow and Kettle Ness. To the north-west of the central Lighthouse are features marked as The Bishop, St. Andrews Well, Altarstanes and Standing Head. Near the Lighthouse, on the western shore, is Mill Door, a natural arch. The island is a designated Nature Reserve with sea-bird colonies on the impressive cliffs. It is less than a half-mile wide.
What I found was that the line of Tinto Hill through Preston Cross extended just misses the southern tip of The May Isle. To the east of Tinto is Scout Hill(NS 965 345), which is a mere 1/32nd of a clock-face-minute(6 degrees) off the Preston Cross - St.Adrian's Chapel line(0.188 degrees).
The bunch of angles range from 46.6 to 47.6 degrees to O.S grid north, which could be taken as being approximately 43 degrees north of east. This is possibly a midsummer sunrise line, if looking north-east from Tinto, or from Preston to the May Isle, across the Firth of Forth. At latitude 55/56 north, midsummer sunrise is approximately 45 degrees dependent on altitude. There is also a minor allowance required for the O.S. grid being 'normal' to true-north at 2 degrees west(Berwick upon Tweed). As this line is roughly in the area of 3 degrees west the adjustment would be minimal, and too complex for me to account for. It would seem likely therefore that midsummer sunrise from Preston Cross, or nearby Tower, would occur over the May Isle. The May Isle I am sure could be seen from the Tower. It would be interesting to get photo/video of the midsummer sunrise from the Tower. Perhaps next year, but access would need to be arranged.
Mid-winter sunrise would be seen in the opposite direction.
Calculations:
Only two included here, Scout Hill to Preston Cross, and Preston Cross to St. Adrian's Chapel.
1. Scout Hill/Preston Cross:
2965.23 6345.47 Scout Hill
3391.27 6740.57 Preston Cross
---------- ----------
-426.04 -395.10
By Pyhtagoras' theorem:
58105 metres
or 36.1045 miles(E), or 32.2 Miles(S), (20 times phi !?)
angle to grid north, 47.16 degrees, (426.04/395.1 = 1.0783; which is tan 47.16deg.)
2. Preston Cross/St. Adrians Chapel, May Isle
3391.27 6740.57 Preston Cross
3658.68 6990.19 St. Adrian's Chapel
---------- ----------
-267.41 -249.62
By Pythag. theorem:
365812 metres (120017 feet)
or 22.73 miles(E), or 20.273 miles(S)(remarkably 20 times the Comma of Pythagoras, 1.0136433, to within 99.999%, or 9.5 inches!!!)
[5/08/08 - just noticed that 22.73 miles(E) is close to 13*'square-root three', 22.5167 miles(E), after doing the following post on Bornholm! This is found to be the distance from Christianso to Nylars! I shall come back to this! The discrepancy is 375 yards, so something may show! TG.]
angle to grid north; 46.97 degrees.
angles difference: 47.16 - 46.97 = 0.19 deg., (1/32nd of one c.f.m.)
[Although not included in these calculations, the distance from Tinto Hill to St. Adrian's Chapel is 314034 feet, a 99.96% correlation with calculator pi, or 99.92% of 22/7.
A circle of this radius would have a circumference of 373,7 miles(E), or 333.3 miles(S).]
Tinto shall be mentioned in following posts, as well may The May be.
I shall do a google map for this line, but I will, no doubt, play about with a bit to see what turns up, using Google Maps and G-Earth.
[When I started my investigation, I was working with 1:25,000 scale maps, and the Isle of May was too far north of Lothian, as was Fife, and so no casual links could be made. The same was true for Tinto Hill, but to the south. It was when I was living in Selkirk that Tinto came to my awareness, as the part of a grid I shall be describing soon.]
The full grid references I shall use:
2952.75 6343.79 Tinto Hill
2965.23 6345.47 Scout Hill, a hill a mile to the east of Tinto, which is found to be a more exact point in line with the southern point on The May Isle.
3391.27 6740.57 Preston Cross, {unicorn}
3658.68 6990.19 St. Adrian's Chapel, May Isle.
3662.83 6988.49 South Ness, May Isle.
3658.68 6990.19 May Isle, St. Adrian's Chapel. The May Isle is roughly at 45 degrees to grid, from North-west to south-east and is a bit more than the diagonal of a grid kilometre square, or a mile approximately. The range is from North Ness {NT 651 999} to South Ness (NT 662 988}.
Marked features on the Island include, between St.Adrian's Chapel and South Ness, Pilgrim's Haven, Pilgrim's Well, Maiden Hair, The Pillow and Kettle Ness. To the north-west of the central Lighthouse are features marked as The Bishop, St. Andrews Well, Altarstanes and Standing Head. Near the Lighthouse, on the western shore, is Mill Door, a natural arch. The island is a designated Nature Reserve with sea-bird colonies on the impressive cliffs. It is less than a half-mile wide.
What I found was that the line of Tinto Hill through Preston Cross extended just misses the southern tip of The May Isle. To the east of Tinto is Scout Hill(NS 965 345), which is a mere 1/32nd of a clock-face-minute(6 degrees) off the Preston Cross - St.Adrian's Chapel line(0.188 degrees).
The bunch of angles range from 46.6 to 47.6 degrees to O.S grid north, which could be taken as being approximately 43 degrees north of east. This is possibly a midsummer sunrise line, if looking north-east from Tinto, or from Preston to the May Isle, across the Firth of Forth. At latitude 55/56 north, midsummer sunrise is approximately 45 degrees dependent on altitude. There is also a minor allowance required for the O.S. grid being 'normal' to true-north at 2 degrees west(Berwick upon Tweed). As this line is roughly in the area of 3 degrees west the adjustment would be minimal, and too complex for me to account for. It would seem likely therefore that midsummer sunrise from Preston Cross, or nearby Tower, would occur over the May Isle. The May Isle I am sure could be seen from the Tower. It would be interesting to get photo/video of the midsummer sunrise from the Tower. Perhaps next year, but access would need to be arranged.
Mid-winter sunrise would be seen in the opposite direction.
Calculations:
Only two included here, Scout Hill to Preston Cross, and Preston Cross to St. Adrian's Chapel.
1. Scout Hill/Preston Cross:
2965.23 6345.47 Scout Hill
3391.27 6740.57 Preston Cross
---------- ----------
-426.04 -395.10
By Pyhtagoras' theorem:
58105 metres
or 36.1045 miles(E), or 32.2 Miles(S), (20 times phi !?)
angle to grid north, 47.16 degrees, (426.04/395.1 = 1.0783; which is tan 47.16deg.)
2. Preston Cross/St. Adrians Chapel, May Isle
3391.27 6740.57 Preston Cross
3658.68 6990.19 St. Adrian's Chapel
---------- ----------
-267.41 -249.62
By Pythag. theorem:
365812 metres (120017 feet)
or 22.73 miles(E), or 20.273 miles(S)(remarkably 20 times the Comma of Pythagoras, 1.0136433, to within 99.999%, or 9.5 inches!!!)
[5/08/08 - just noticed that 22.73 miles(E) is close to 13*'square-root three', 22.5167 miles(E), after doing the following post on Bornholm! This is found to be the distance from Christianso to Nylars! I shall come back to this! The discrepancy is 375 yards, so something may show! TG.]
angle to grid north; 46.97 degrees.
angles difference: 47.16 - 46.97 = 0.19 deg., (1/32nd of one c.f.m.)
[Although not included in these calculations, the distance from Tinto Hill to St. Adrian's Chapel is 314034 feet, a 99.96% correlation with calculator pi, or 99.92% of 22/7.
A circle of this radius would have a circumference of 373,7 miles(E), or 333.3 miles(S).]
Tinto shall be mentioned in following posts, as well may The May be.
I shall do a google map for this line, but I will, no doubt, play about with a bit to see what turns up, using Google Maps and G-Earth.
Tuesday 17 June 2008
Salisbury Crags Face and general area

In July 2006 I moved to Inverkeithing, and I had to get the train into Edinburgh, then get to Portobello Road to pick up the taxi for my nightshift. During the Festival I sometimes walked, from the staion, if the weather was nce. One time when crossing the Forth Rail Bridge there was a cloud formation in the form of a head over Burntisland facing north-east, with a trail of cloud over the Forth.
Looking at the photo now, at this scale the cloud face is none too clear!
Whatever the processes going on in my brain, walking into Holyrood Park between the Parliament Building and the Palace, taking a few photos of the crags and the lion carving near the car-park, gazing towards the crags at their eastern end, I took a shot of the interesting rock formations. Later when I downloaded the photos I was looking at this photo and saw a face formed by the crags rock. I could also see another two faces to the left.
I have been drawn back there many times since, examining the crags and verifying to myself that these are real stone formations and are identifiable in all light conditions. One in particular is very impressive, and is about 30 feet in scale.
Below is a link to a web-album with more photos of this and the other faces, and some of broom, and gorse in bloom this May, and some of St. Margaret's Loch and St. Anthony's Chapel ruin. This area covers the extent of spread of all the lines considered in the section on Schiehallion through Arthurs' Seat to The Eildon Hills:
 |
| gorse/whin |
Thursday 1 May 2008
Lindisfarne to Duart Castle, Mull
The work of William S. Buehler has been mentioned previously, and Bill has been highlighting a grid possibility incorporating the River Almond and Cramond at its mouth. He has also in the past described a system using the Lindisfarne (NT 136 422) - Duart Castle (NM 748 353), on the island of Mull, extending from there to both Iona and Staffa.
Whilst in Google Maps I decided to plot this line and see where it crossed the entral area of my focus, and what else was included.
Using several points I calculated their relationships with both Lindisfarne and Duart Castle. Omitting detailed calculations for now, I found that the line from Lindisfarne to Duart Castle passed between Arthurs Seat and Inchcolm, and precisely the northern tip of Cramond Island (NT 197 787), some 68 yards offshore, at a distance from Lindisfarne of 63.5 miles(E).
(As I did this exercise I saw the line as a guitar string being plucked and vibrating between Arthurs Seat and Inchcolm, like a gate mechanism, limiting the pitch of the string.)
Other points of interest on this line Yester Castle, Musselburgh, Devilla Forest/Tulliallan Castle, Port Of Menteith, Ben Vorlich.
The line is on the Google Map on the Preston Cross triangle page. I need to limit the number of G-Maps I include as they slow loading down too much!
This is just a brief note on this topic, for now!
Whilst in Google Maps I decided to plot this line and see where it crossed the entral area of my focus, and what else was included.
Using several points I calculated their relationships with both Lindisfarne and Duart Castle. Omitting detailed calculations for now, I found that the line from Lindisfarne to Duart Castle passed between Arthurs Seat and Inchcolm, and precisely the northern tip of Cramond Island (NT 197 787), some 68 yards offshore, at a distance from Lindisfarne of 63.5 miles(E).
(As I did this exercise I saw the line as a guitar string being plucked and vibrating between Arthurs Seat and Inchcolm, like a gate mechanism, limiting the pitch of the string.)
Other points of interest on this line Yester Castle, Musselburgh, Devilla Forest/Tulliallan Castle, Port Of Menteith, Ben Vorlich.
The line is on the Google Map on the Preston Cross triangle page. I need to limit the number of G-Maps I include as they slow loading down too much!
This is just a brief note on this topic, for now!
Tuesday 29 April 2008
Schiehallion - Inchcolm

To complete this exercise I shall now compare the Inchcolm line with the Arthurs Seat line and perhaps some others. I am interested to see if there is some sort of system evident centered on Schiehallion.
2713.833 7547.736 Schiehallion
3189.700 6826.690 Inchcolm Abbey
--------- ----------
-475.867 0721.946
By Pythagoras theorem: 0863.92, which converts to 53.6815 miles(E), and 47.878 miles(S)
The angle to O.S Grid: 33.42352 degrees
The initial impulse for this exercise was noticing that the the lines from Schiehallion to Arthurs Seat and Inchcolm were separated by a very close approximation of one degree.
One of the findings of Haagensen and Lincoln, on Bornholm was a one degree construct, which was pointed out as having potential relevance as an example of a Medieval solution to a fact of geometric drawing that it is impossible to divide an angle into three, using the classic instruments of pen, compass and straight-edge. This is a purely technical problem, in that we use 360 degrees in a circle, which has a base of three, so that an angle of one degree is impossible under Pythagorean/Sacred geometry principles. I shall be discussing Bornholm later.
The angles from Schiehallion to:
34.4544 degrees: Arthurs Seat
33.4235 degrees: Inchcolm Abbey
---------
01.0309 degrees
0.0309 derees is 1/194th of one-clock-face minute, the tangent of this angle being, 0.00054, which at 54 miles(E) is 154 feet, or 50 yards approximately. Certainly on the island.
I then checked the Preston Cross line and the Galachlaw phi-point line
Schiehallion to:
40.0061 degrees: Preston Cross
31.9024 degrees: Galachlaw phi-point
---------
08.1037 degrees
Now, 8 degrees is easily divide three times to give one degree; and 8.1037 divide three times gives: 1.0129625 deg.
0.0129625 deg (1/463rd of one c.f.m.) has a tangent of 0.00022624, and at 63 miles(E) is 75 feet, or 25 yards.
So, some intriguing results but not a major concern at this moment.
8 degrees is 1/45th of a circle, so may be related to the circle divided into 15, 45 being three times fifteen. Perhaps relevant!
Friday 11 April 2008
Schiehallion - Galachlaw - Rubers Law
Back in the year 2000, I was driving south to England from Selkirk, early morning, to be in Lichfield for 9.30am.
From Hawick I took the A6088 towards Bonchester Bridge, and as the road took a turn east just after Kirkton, I was stunned by the hill silhouetted by the early dawn light:

On the way back later that day, I took another photo of the same hill:

I confirmed this hill to be Rubers Law, O.S grid reference: NT 579 155.
I had been working on some geometry, see previous Schiehallion - Eildon line post, and was discovering the landscape of the Borders as I went. Rubers Law was part of the discovery process. I can't quite describe the feeling of shocked awe when I turned east that morning to see the hill in the dawn light, dark and brooding in silhouette. I had to check the maps to see if and where it fitted in. With great amazement I found it to be in a direct line with Schiehallion and Galachlaw, the entre of the original pentagonal system previously described. Especially so since I had already confirmed the Schiehallion -Arthurs Seat - Eildon line.
When I got round to doing the detailed calculations, I was even more amazed to find that Galachlaw was indeed very close to the Phi-point.
A few calculations to show this:
Grid References (full, and normal forms)):
2713.83 7547.74 Schiehallion summit NN 714 547
3253.65 6683.21 Galachlaw cairn NT 253 683
3249.37 6687.44 Water Works mast( exact Phi-point) NT 249 686
3580.35 6155.75 Rubers Law summit NT 579 155
Schiehallion:

first calculation; Schiehallion - Rubers Law:
2713.83 7547.74 Schiehallion
3580.35 6155.75 Rubers Law
--------- ----------
0866.52 1391.99
By Pythagoras' theorem; 1639.66
which converts to 101.88 miles(E), and 90.87 miles(S)
The angle to grid north is 31.9024 degrees, using the tangent of the two calculated values above.
Second Calculation; Schiehallion - Galachlaw cairn:
2713.83 7547.74 Schiehallion
3253.65 6683.21 Galachlaw cairn
--------- ----------
0539.82 0864.53
By Pythag. 1018.22
which converts to 63.33miles(E)and 56.48miles(S)
angle to grid; 31.98075 deg.
using the English miles distances of both we ind the relationship to be 99.424% of Phi:
101.88/63.33 = 1.60872, which is 99.424% of 1.618034.
Galahlaw Cairn:

The exact Phi-point proves to be some 660 yards to the north west of the cairn, at point (3249.37 6687.44), which is in the Water works where a Mast is erected, normal grid reference NT 249 686.
view of gap between Hillend fort on right and Galachlaw with Water Works Mast to the left:

This mast can be seen to the left of this photo, with Hillend Fort to the right.
Comment:
All I can say about this is that it was around this time that I came to strongly accept a 'sense of process' involving time and place, and which I for sure am not in control of. It is not just an excuse for me to be lazy in presenting all this material, it has taken years to get to, and I have learned to accept patience as an essential. All the geometry and correlations have in a sense been presented as and when 'this process' deems necessary. I no longer question this, it just happens when it does.
supplementary
When plotting this line on Google Maps, I checked Fordell Castle which I had noted originally was on this line, and on calculation was found to be at the centre, Fordell Hill precisely, within the estate. Fordell was the home/seat of Nicholas 'Nicky' Fairbairn, a Tory MP, government Minister and somewhat extrovert.
As Galachlaw is at the phi-point of the line, there is another equivalent on the other side of the centre-point. On examination and confirmed by calculation, it was found to be White, or Hood Hill, NO 042 018, near Tullibole Castle, by Crook of Devon.
There is also a radio/electronics mast on Hood Hill!? (Once is chance, twice is coincidence...!)
(There was reported that a sign-post in Crook Of Devon had neatly printed under it: 'Twinned with Thief Of Baghdad'! - btw! lol)
In addition it was noted that Lauriston Castle is on this line, and Cramond Island. Lauriston Castle came to my attention in connection with John Napier of Merchiston, an Alexander Napier having owned it. Lauriston Castle proved subsequently to be a geometric node, and still to be described.
Cramond has been highlighted recently by Bill Buehler, in connection with the Roman lion staue with man in its mouth, which I also linked with John Napier, or the double lion-gate at Merchiston, in an e-mail exchange!
From Hawick I took the A6088 towards Bonchester Bridge, and as the road took a turn east just after Kirkton, I was stunned by the hill silhouetted by the early dawn light:
On the way back later that day, I took another photo of the same hill:

I confirmed this hill to be Rubers Law, O.S grid reference: NT 579 155.
I had been working on some geometry, see previous Schiehallion - Eildon line post, and was discovering the landscape of the Borders as I went. Rubers Law was part of the discovery process. I can't quite describe the feeling of shocked awe when I turned east that morning to see the hill in the dawn light, dark and brooding in silhouette. I had to check the maps to see if and where it fitted in. With great amazement I found it to be in a direct line with Schiehallion and Galachlaw, the entre of the original pentagonal system previously described. Especially so since I had already confirmed the Schiehallion -Arthurs Seat - Eildon line.
When I got round to doing the detailed calculations, I was even more amazed to find that Galachlaw was indeed very close to the Phi-point.
A few calculations to show this:
Grid References (full, and normal forms)):
2713.83 7547.74 Schiehallion summit NN 714 547
3253.65 6683.21 Galachlaw cairn NT 253 683
3249.37 6687.44 Water Works mast( exact Phi-point) NT 249 686
3580.35 6155.75 Rubers Law summit NT 579 155
Schiehallion:

first calculation; Schiehallion - Rubers Law:
2713.83 7547.74 Schiehallion
3580.35 6155.75 Rubers Law
--------- ----------
0866.52 1391.99
By Pythagoras' theorem; 1639.66
which converts to 101.88 miles(E), and 90.87 miles(S)
The angle to grid north is 31.9024 degrees, using the tangent of the two calculated values above.
Second Calculation; Schiehallion - Galachlaw cairn:
2713.83 7547.74 Schiehallion
3253.65 6683.21 Galachlaw cairn
--------- ----------
0539.82 0864.53
By Pythag. 1018.22
which converts to 63.33miles(E)and 56.48miles(S)
angle to grid; 31.98075 deg.
using the English miles distances of both we ind the relationship to be 99.424% of Phi:
101.88/63.33 = 1.60872, which is 99.424% of 1.618034.
Galahlaw Cairn:
The exact Phi-point proves to be some 660 yards to the north west of the cairn, at point (3249.37 6687.44), which is in the Water works where a Mast is erected, normal grid reference NT 249 686.
view of gap between Hillend fort on right and Galachlaw with Water Works Mast to the left:
This mast can be seen to the left of this photo, with Hillend Fort to the right.
Comment:
All I can say about this is that it was around this time that I came to strongly accept a 'sense of process' involving time and place, and which I for sure am not in control of. It is not just an excuse for me to be lazy in presenting all this material, it has taken years to get to, and I have learned to accept patience as an essential. All the geometry and correlations have in a sense been presented as and when 'this process' deems necessary. I no longer question this, it just happens when it does.
supplementary
When plotting this line on Google Maps, I checked Fordell Castle which I had noted originally was on this line, and on calculation was found to be at the centre, Fordell Hill precisely, within the estate. Fordell was the home/seat of Nicholas 'Nicky' Fairbairn, a Tory MP, government Minister and somewhat extrovert.
As Galachlaw is at the phi-point of the line, there is another equivalent on the other side of the centre-point. On examination and confirmed by calculation, it was found to be White, or Hood Hill, NO 042 018, near Tullibole Castle, by Crook of Devon.
There is also a radio/electronics mast on Hood Hill!? (Once is chance, twice is coincidence...!)
(There was reported that a sign-post in Crook Of Devon had neatly printed under it: 'Twinned with Thief Of Baghdad'! - btw! lol)
In addition it was noted that Lauriston Castle is on this line, and Cramond Island. Lauriston Castle came to my attention in connection with John Napier of Merchiston, an Alexander Napier having owned it. Lauriston Castle proved subsequently to be a geometric node, and still to be described.
Cramond has been highlighted recently by Bill Buehler, in connection with the Roman lion staue with man in its mouth, which I also linked with John Napier, or the double lion-gate at Merchiston, in an e-mail exchange!
Monday 7 April 2008
Google Maps trial
First attempt at drawing lines on Google Maps. This is the Schiehallion to Eildon Hills North line:
View Larger Map
It seems to be slightly off at Arthurs Seat in comparison to calculations and Google Earth. Needs to be considered further!?
I have also marked Newtongrange and Borthwick on this line now.
View Larger Map
It seems to be slightly off at Arthurs Seat in comparison to calculations and Google Earth. Needs to be considered further!?
I have also marked Newtongrange and Borthwick on this line now.
Monday 24 March 2008
sense of place - photo-album
After all that math of the previous posts, I have spent the day 'playing' with photos, and have managed to upload some as a web-album in Picasa.
Here's some photos of Lothian and the Borders of Scotland, un-captioned as of yet, and pretty much random.
Here's some photos of Lothian and the Borders of Scotland, un-captioned as of yet, and pretty much random.
Friday 7 March 2008
Schiehallion alignments part one - Arthurs Seat to Eildon

The grid references to be used in this section are:
2713.833 7547.736 Schiehallion summit(S)
3275.280 6729.430 Arthurs Seat(AS)
3554.330 6329.100 Eildon north Ring Fort(E)
3333.750 6642.000 Newtongrange Church(N)
3580.350 6155.750 Rubers Law(RL)
3253.645 6683.210 Galachlaw Cairn(G)
3249.370 6687.440 Water Works, calculated exact golden-section point near Galachlaw
3189.702 6826.692 Inchcolm Abbey(I)
The calculations to follow on the three lines on the drawing. What I shall show is: 1) that Schiehallion, Arthurs Seat and Eildon Ring Fort, and Newtongrange Church are all on a straight line, within very tight margins.
2) That Galachlaw Cairn, the center of the original penta-system, is very close to the EXACT phi-point(golden section/mean) between Schiehallion summit and Rubers Law summit. The exact point is in fact in the local water-works, where a radio mast stands(!?).
3) That Inchcolm Abbey is at one degree, very lose, to the Arthurs Seat line, at Schiehallion, which may be relevant.
On the diagram, it can be seen that the Inchcolm line extends to a point labelled (FC), this is Fatlips Castle near Minto in the Borders. The calculations to Fatlips have not been included here.
The axis of the original penta-system is shown, from Roslin(R) through Galahlaw(G) to Inchcolm(I).
There is a vertical line, indicating what has been called the 'Roseline', or in Bill Buehler's terminology, the Tavhara, with Dryhope Tower(DT) at the bottom, and Seafield Tower(ST) at the top, both on the circle circumference, centre St Mary's chapel(St M), radius 20 miles. This is still to be explained in detail.
Part 2
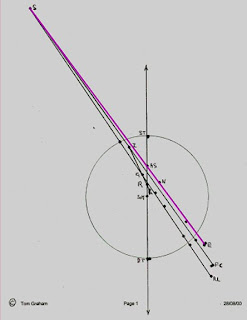
The line highlighted in the diagram, between Schiehallion(S) and The Eildon Hills(E), runs through the Arthurs Seat(AS) area, with a ratio of 2:1, and also includes Newtongrange Church(N), which is one of the determining points of the Rennes Le Chateau radius as determined by Henry Lincoln, with Mavisbank as centre.
Schiehallion:
The Eildon Hills, known to the Romans as Trimontium, has Melrose Abbey nestled in the low ground near the river Tweed. The example given here uses Eildon North, with a large ring-fort on its summit, and was used as a signal station by the Romans.
Eildon Hills:
I shall later also use Eildon Mid-hill, which has an O.S. trig-point on its summit.
Arthurs' Seat also has a trig-point on its summit, and it is the summit which really defines the 'Roseline', through Rosslyn Chapel(R), and is shown on the diagram, with centre at St. Mary's Chapel(St.M), and a 20mile radius circle, with Seafield Tower(ST) on the 'Roseline' to the north, and Dryhope Tower(DT) to the south. The Arthurs Seat complex covers quite a lage area, from Holyrood Abbey/Palace/Parliament Building, St. Anthony's chapel, Dunsappie Fort, Duddingston Church, Crow Hill and Whinny Hill, and Salisbury Crags. There is a lot to consider and this post has been somewhat delayed due to my need to compare a whole set of calculations between Arthurs' Seat and the Eildon Hills, with some interesting correspondences and ratios of distances and angles.
Arthurs Seat, from Hillend Fort,(very important geometric point, to be discussed), over Galachlaw, (centre of original pentagon, and to be discussed in the Schiehallion to Rubers Law line, Galachlaw at Phi-point):
Schiehallion summit is taken as a constant. It has already been seen to lie on the hypotenuse of the Preston Cross triangle.
All three sites are special, with their associated myths and legends, in a sense they are all considered 'magic' mountains.
Using the Grid references listed in the previous post, and using the same procedure as before:
Calculation (1)
2713.833 7547.736 Schiehallion
3275.280 6729.430 Arthurs Seat
------------ ------------
0561.447 0840.167
By Pythagoras theory;
0992.395
which converts to;
61.664556 miles(E); or 54.998 miles(S)
The angle to the O.S. grid, again using the tangent of the ratio of the two derived grid components is 34.4544 degrees
Calculation(2)
2713.833 7547.736 Schiehallion
3554.330 6329.100 Eildon North(ring-fort)
------------ ------------
0840.497 1218.636
By Pythag; 1480.375
which converts to;
91.9862 miles(E); or 82.042 miles(S)
Angle to O.S.grid; 34.59415 degrees
First of all the angles to grid are:
34.45440deg.
34.59415deg.
------------
0.13975deg. difference
This is 1/43rd of one clock-face-minute(cfm), (reminder that one cfm is six degrees).
This discrepancy at Arthurs' Seat summit is some 265 yards.
The exact line runs to the north east, between the summit and Dunsappie fort. If the Arthurs' Seat line is used and projected to the Eildon, it passes through the gap between Eildon North and Mid-hills.
The Schiehallion/Eildon North line runs through the gap between Arthurs Seat summit and this stone, convenient marker(!), on Whinny Hill:
So, Schiehallion, Arthurs' Seat and the Eildon Hills are in a straight line!
The distance ratio is 61.664556:91.9862 = 2:2.98344(99.45% of 3)
The exact distance of Arthurs Seat to Schiehallion should be 61.324 miles(E) for a 3:2 ratio. A discrepancy of 600 yards, or 0.34 miles(E), north towards St. Anthony's Chapel and Holyrood Abbey.
Holyrood Abbey/Palace, lower foreground and St. Anthony's Chapel, the ruin left centre:
This is relevant perhaps to geometrical grid work, the 3:1 ratio having shown up elsewhere. More needs to be done on this aspect at a later date. Just to note in passing that the diagonal of a 3 by 1 grid is the square root of ten!
William Buehler(Bill) has recently described a temple format using this ratio, and I have found it to be in use in a grid based on the twenty mile radius in the diagram, which was first defined, to my knowledge, by Bill.
Enough on that topic for now!
Next to consider the position of Newtongrange church:

2713.833 7547.736 Schiehallion
3333.750 6642.000 Newtongrange Church
----------- ------------
0619.917 905.736
By Pythag. 1097.568
converts to; 68.1997 miles(E); or 60.827 miles(S)
Angle to O.S. grid: 34.389 degrees.
Comparing this angle to that of Schiehallion/Eildon North:
34.59415 Schiehallion/Eildon(N)
34.38900 Newtongrange churh
-------------
0.20515 deg. (1/29th cfm, or some 430yards at Newtongrange) A quarter of a mile may seem a lot, but at this scale it is in reality not much, and later I shall show that Newtongrange is more accurately in line with Eildon Mid-hill and Arthurs Seat.
Keeping this in bite-sized chunks I shall leave this here for now!
Supplementary one
The exact 3 by 1 ratio mentioned in the previous post, existing between Schiehallion, Arthurs Seat and Eildon North can be shown to be just over 60 yards from St Anthony's Chapel, O.S.grid reference (3275.755 6737.100).
I'm not bothering with full calculation sets here, but shall give O.S.grid references used, so can be verified by anyone with a calculator, and an interest!
St. Anthony's chapel is also 323606 feet, (61.289 miles(E)) from Schiehallion, a 2*Phi relationship.
2*Phi is 2 * 1.618034 = 3.236068, hence correspondence is 99.9997%, ignoring decimal points.
The calculated distance from St. Anthony's Chapel and Eildon North is 30.698 miles(E), or 162084 feet, a discrepancy of 93.5 yards from perfect of 161803.4 feet
As calculated in previous post, the exact 2:3 point at Arthurs Seat is 61.324 miles(E) from Schiehallion, and St.Anthony's Chapel is 61.289 miles(E), the difference being 61.6 yards.
The angle to O.S.grid is found to be 34.7292 degrees, and Duddingston Church (O.S. grid ref. used 3283.113 6726.172), an angle of 34.72 degrees, at a distance of 62.1075 miles(E).
These two angles are nearly identical, (a difference of 0.0092 deg, at a distance of 0.8185 miles(E), or 4321 feet, or 1440 yards (!?) is 0.7 feet, exact given the limit of practicality in my method. Anything within ten yards is too close to differentiate!)
So, Duddingston Church and St. Anthony's Chapel are in direct line with Schiehallion summit!
Also, St. Anthony's Chapel is also remarkably at the exact Phi harmonic distance in feet, from Schiehallion, and also marks the 2:3 point!!
And a final point of note concerning Duddingston Church and St. Anthony's Chapel:
the ratio of their distances from Schiehallion is: 62.1075 : 61.289, which is 1.013355 : 1! This ratio is greater than 99.97% of the Comma of Pythagoras as found in the work of Robert Temple, The Sirius Mystery, for example (page 24); the ratio of 3^12 : 2^19, or 531,441 : 524,288, or 1.0136433.
Duddingston Church and loch:
So, the area between both can be considered as the area of harmonic fluctuation between the ideal and the real in geometric terms, in accordance with the theories of the Pythagoreans. This area contains most of the Arthurs Seat area, including the summit. I consider this to be a perfect example of what I term a 'unit point area', which varies in size with distance, especially at special sites like Arthurs Seat and the Eildon.
Also, St. Anthony's Chapel is situated very close to the projection of the Tavhara line mentioned previously, to the north of Arthurs Seat summit.
Thus St. Anthony's Chapel can be considered a very special geometric marker.
Duddingston, too, is also a special point, including the area of the loch which it sits by. The exact line from Schiehallion to Eildon North passes by the western end.
added 20/03/08. Taking the tangent of the difference in angles between Duddingston and St.Anthony's to Schiehallion:
34.792 - 34.72 = 0.0092, the tangent of which is 0.00016057, times the distance from Schiehallion to St. Anthony's Chapel, 61.289 miles(E), equals 0.0098412 miles(E), which equals 51.9615eet, or 17.32049908 yards, which is an incredible 99.99995% harmonic of the square root of three!
I have difficulty coming to terms with a finding like this. It implies, an intent in the positioning of St.Anthony's and Duddingston, with an accuracy so great to beggar belief. Root three is of course an integral component of an equilateral triangle, namely the altitude in relation to the side.
The correspondences between St. Anthony's chapel and Duddingston and Schiehallion are astonishing, and leave much room for thought.
Supplementary two
As mentioned in main post, Newtongrange Church is more exactly in line with Arthurs Seat summit and Eildon Mid-Hill summit (O.S.grid reference used: 3548.19 6323.03)
Arthurs Seat to Eildon Mid-Hill, the distance is 30.418 miles(E), and the angle to O.S. grid is; 33.8826 degrees.
Newtongrange Church to Eildon Mid-Hill, the distance is 23.88252 miles(E), and the angle to O.S. grid; 33.9125 degrees.
The distance from Arthurs Seat and Newtongrange Church is some 6.5355 miles(E), and the difference in angle, 0.03 degrees; and using the tangent of this angle a discrepancy of 18 feet, near enough to be considered exact! (0.03degrees is 1/200th of one clock-face-minute!)
Finally, worthy of note, perhaps, is that there is found to be a 'near' pi, (99.97%) relationship between the two distances:
A.S. to E.M.-H.; 30.418 miles(E)
N.C. to E.M.-H.; 23.88252 miles(E)
23.88252/30.418 = 0.785144322, multiplied by four gives; 3.1406, (99.97% calculator pi, or 99.93% of 22/7, a commonly used version).
Supplementary three
Consideration of a significant geometric centre, already discussed in the Borthwick series of posts, namely Borthwick Church and Castle.
The references in the form used here are:
Borthwick Church 3368.785 6596.075
Borthwick Castle 3370.00 6597.597
I do not intend giving the full calculations here, just to point out that the exact line from Schiehallion to Eildon North, is at an angle to the O.S. grid of 34.594 degrees.
The angles to Borthwick Church, 34.5365 degrees, and to Borthwick Castle, 34.62 degrees.
From this it can be seen that the line passes between the two Borthwick points. It passes some 58 yards from the castle, and 126 yards from the church.
The distances are 71.7844 miles(E), or 64.024 miles(S) for Borthwick Church, and 71.765 miles(E), or 64.0067 miles(S). for Borthwick Castle.
The distance in Scottish miles, of 64 miles(S), is worthy of note, being 8 squared!
So, the line from Schiehallion to Eildon North passes through Borthwick.
Borthwick Castle, left, Church, right, looking south-east towards The Eildon, way beyond horizon:
This is looking north-west over Arthurs Seat, summit just visible, towards Schiehallion, faintly discernible on horizon, (click on image for larger version). Borthwick is on other side of foreground rise, not visible. This is taken from the point on the A7 south o Middleton, where the line crosses:

Finally, there are several points on this line, from a scan of Google Earth, but not calculated:
Drum estate, and the corner at The Wisp, near Danderhall, and Edmonstone House, just south of Arthurs Seat. North, Starbank Park on the coast, and Aberdour harbour on the Fife coast.
Extending south to the North Sea, the line passes through Lincolnshire and The Wash. A crop circle was found in Lincolnshire in Google Earth, very close the line. This is an area which a fellow researcher is looking at.
Main Finding from investigation, (so far)
The main finding rom this investigation, so far, is that Arthurs Seat/Holyrood Park sits at the 2/3rds distance between Schiehallion and The Eildon Hills. St.Anthony's Chapel in Holyrood Park can be assumed as the marker point. Not only that, but St. Anthony's Chapel is 'exactly' 323,606 feet from Schiehallion, and approximately 161,804 feet from Eildon North. Phi, (golden section) is 1.618034, so both distances are an exact harmonic of Phi!
This is a simple representation of the three by one rectangle, using the diagonal as the Schiehallion - Eildon line. I could have done it as the side of the rectangle, but chose the diagonal, as later I shall be discussing the 3 by 1 rectangle in connection with a grid, which has a 3 by 1 diagonal as a baseline for a very special geometric system. The diagonal of a 3 by 1 rectangle is in fact, square-root ten.(By Pythagoras, (3^2 plus 1 equals 10. The diagonal is thus square-root 10)
Subscribe to:
Posts (Atom)